СИСТЕМНЫЕ ОБРАЗОВАНИЯ: ИНФОРМАЦИЯ И ОТРАЖЕНИЕ

Вяткин В.Б.

СТРУКТУРНАЯ ОРГАНИЗАЦИЯ ЭЛЕКТРОННЫХ СИСТЕМ
АТОМОВ ХИМИЧЕСКИХ ЭЛЕМЕНТОВ
В СВЕТЕ СИНЕРГЕТИЧЕСКОЙ ТЕОРИИ ИНФОРМАЦИИ

// Ergo. Проблемы методологии междисциплинарных исследований и комплексного обеспечения
научно-исследовательской деятельности. Вып. 4. Екатеринбург: УрО РАН, 2005

-------------------------------------------------------------------------------------------------------------------------

2. Структурная организация электронных систем
в плоскости орбитального квантового числа

Электронные системы атомов химических элементов состоят из конечного множества электронов, число которых равно порядковому номеру элементов (Z) в периодической системе Д.И. Менделеева. Рассматривая эти системы в плоскости какого-либо квантового числа, можно по значениям последнего выделять системные объекты и с помощью R-функции (8) оценивать соответствующую структурную организацию систем.

В настоящем разделе объектом нашего анализа будет являться структурная организация электронных систем атомов в плоскости орбитального квантового числа (). При этом в качестве системных объектов перед нами будут выступать совокупности электронов с одинаковым значением или, иначе говоря, – s, p, d, f совокупности (напомним, что символами s, p, d, f обозначаются электроны со значениями , соответственно). Обозначая количество электронов в указанных совокупностях через методику расчета R-функции в данном случае можно продемонстрировать следующим образом.

Возьмем для примера атом криптона , электронная конфигурация которого имеет вид:

.

Здесь.......................................

Подставляя эти значения в формулу R-функции (8) и, учитывая, что , получаем:

.

По данной методике проведен расчет значений R-функции в плоскости орбитального квантового числа для электронных систем всех атомов химических элементов с порядковым номером , результаты которого, а также распределение электронов в атомах по s, p, d, f совокупностям приведены в табл. 1 [10].

На рис. 5 представлен график зависимости полученных значений R-функции от порядкового номера химических элементов в периодической системе Д.И. Менделеева.

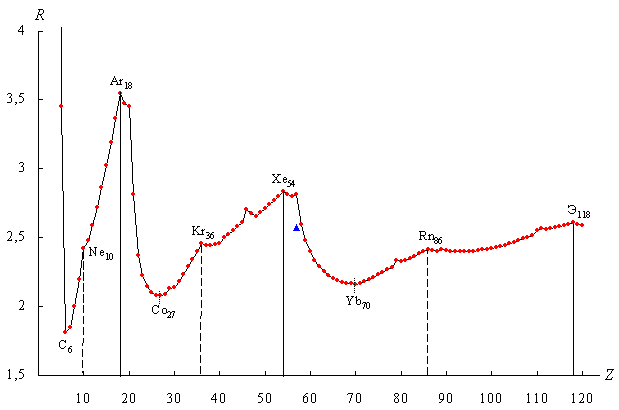
- значение R-функции при

Рис. 5. График R-функции электронных систем атомов химических элементов
в плоскости орбитального квантового числа

График имеет ярко выраженный периодический характер и включает в себя четыре основных периода ( Т ), границы которых проходят по “региональным” максимумам R-функции [11], наблюдаемым у химических элементов с порядковыми номерами Z = 2, 18, 54, 118 [12]. Количество элементов в периодах (m(T_N ), N – номер периода) соответственно равно:

................................................................................. (11)

Так как объектом нашего анализа изначально является распределение электронов в атомах по значениям орбитального квантового числа, а R-функция по определению (8), характеризует структурную организацию дискретных системных образований, то дадим этим периодам общее название – орбитальные периоды структурной организации электронных систем атомов химических элементов. На протяжении второго, третьего и четвертого орбитальных периодов график R-функции имеет форму бегущей волны, то есть, наблюдается общий резкий спад значений в начале периода и относительно плавное их повышение при движении к его концу. В связи с этим второй, третий и четвертый периоды будем называть также орбитально-волновыми периодами.

При более детальном рассмотрении графика во всех орбитально-волновых периодах в поведении R-функции наблюдается еще одна закономерность, которая сводится к следующему. Сначала имеет место последовательное понижение значений, заканчивающееся “региональными” минимумами R-функции у элементов с порядковыми номерами Z = 6, 27, 70. Затем следует возрастание значений, относительно равномерно продолжающееся до достижения “локальных” максимумов у элементов с Z = 10, 36, 86. После этих максимумов значения R-функции претерпевают незначительное понижение (во втором периоде просто существенное замедление возрастания значений), которое сменяется практически монотонным повышением значений, идущим до конца периодов (“региональных” максимумов) и имеющим более плавный характер, чем возрастание до “локальных” максимумов. При этом, по мере возрастания Z, изменение значений в “региональных” и “локальных” максимумах имеет различный характер: значения R-функции в “региональных” максимумах интенсивно снижаются , а в “локальных” максимумах сохраняют относительно постоянное значение
(R = 2,421; 2,457; 2,413). Также нетрудно видеть, что “локальные” максимумы R-функции наблюдаются у элементов с порядковыми номерами равными полусумме порядковых номеров тех элементов, которые обладают смежными с ними “региональными” максимумами. То есть имеем:

.

Отмеченные закономерные особенности поведения R-функции внутри орбитально-волновых периодов позволяют говорить о том, что в структурной организации электронных систем атомов химических элементов, рассматриваемых в плоскости орбитального квантового числа, присутствует еще одна (вторичная) периодичность, которая делит каждый орбитально-волновой период на два полупериода с одинаковым количеством элементов. В соответствии с выражением (11) эти количества элементов в орбитальных полупериодах равны:

.............................................................................(12)

Заканчивая общее описание графика R-функции распределения электронов по значениям орбитального квантового числа, остановим свое внимание на выражении (11). Его анализ показывает, что количество элементов в орбитально-волновых периодах связано с их номером квадратичной зависимостью:

. ............................................................................................(13)

То есть:..............................................

Сопоставление приведенных результатов анализа графика R-функции со структурой периодической системы Д.И. Менделеева позволяет высказать следующее. Первое, что обращает на себя внимание, это то, что все орбитальные периоды и полупериоды структурной организации электронных систем, так же как химические периоды периодической системы, заканчиваются инертными газами, а начинаются следующими за ними химическими элементами. При этом каждый орбитально-волновой период охватывает два химических периода (- номер периода) с одинаковым числом элементов , то есть:

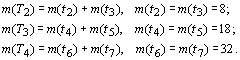....................................................................(14)

Соответственно, все орбитальные полупериоды в точности совпадают с химическими периодами и равны с ними по числу элементов. Поэтому в дальнейшем орбитальные полупериоды будем также обозначать символом t_n.

Из выражения (14) следует, что количество элементов в химическом периоде зависит от того, к какому периоду структурной организации он принадлежит. Так как число элементов во всех орбитально-волновых периодах связано с их номером квадратичной зависимостью (13), то согласно (14) количество элементов в химических периодах имеет следующее выражение:

........................................................................ (15)

Применяя формулу (15) к семи известным химическим периодам периодической системы Д.И. Менделеева, получаем числовой ряд [13]:

2, 8, 8, 18, 18, 32, 32, ..........................................................................................(16)

члены которого в точности соответствуют количеству их элементов. При этом несколько неожиданным является тот факт, что формула (15) оказалась справедливой для первого химического периода. Это позволяет высказать предположение, что первый орбитальный период по своей сущности является орбитально-волновым полупериодом.

Таким образом, выражения (15) и (16), позволяют утверждать, что количество элементов в химических периодах периодической системы Д.И. Менделеева равно удвоенному квадрату номера орбитального периода структурной организации электронных систем, к которым они принадлежат. Также можно констатировать, что, располагая только распределением электронов в атомах химических элементов по значениям орбитального квантового числа, мы, с помощью аппарата синергетической теории информации, воспроизвели периодическую структуру системы Д.И. Менделеева, “априорно ничего не зная о ней”.

Рассмотрим теперь особенности электронных систем атомов в пределах орбитальных периодов их структурной организации и параллельно будем сравнивать эти особенности с периодической системой Д.И. Менделеева. При этом, проводя анализ табл.1, предварительно отметим, что для каждого орбитального периода и полупериода электроны предыдущих периодов и полупериодов составляют фоновую совокупность, переходящую от одного химического элемента к другому. Поэтому объектом нашего анализа будут являться совокупности только новых электронов, образующих тот или иной орбитальный период и полупериод.

Из приведенной таблицы видно, что в каждом орбитальном периоде у атомов химических элементов появляются электроны с новым значением орбитального квантового числа. То есть, в первом периоде наблюдаются только s электроны , во втором периоде дополнительно появляются p электроны , в третьем – d электроны и в четвертом периоде – f электроны . Иначе говоря, во всех орбитальных периодах структурной организации электронных систем атомов химических элементов орбитальное квантовое число принимает ряд значений, максимальное из которых выражается формулой:

, ...................................................................................................(17)

а общее число этих значений равно, соответственно, номеру периода N. При этом в каждом орбитальном полупериоде наблюдаются все N значений орбитального квантового числа, а соответствующее число s, p, d, f электронов в атомах их элементов (как и число самих s, p, d, f элементов) достигает величины:

....................................................................(18)

Анализ выражения (18) показывает, что в орбитальных полупериодах число электронов с данным значением орбитального квантового числа связано с номером орбитального периода, в котором они впервые появились, зависимостью:

. ..........................................................................................(19)

Заменяя на основе выражения (17) в формуле (19) N на , получаем общую формулу числа электронов при данном значении орбитального квантового числа, хорошо известную из курса теории строения атома:

........................................................................................... (20)

Соответственно, число элементов в орбитальном полупериоде, ранее определенное нами посредством визуального анализа графика R-функции как , на основе выражений (17) и (20) конкретизируется в виде формулы:

......................................................................(21)

из которой в отношении числа элементов орбитально-волновых периодов (как и в отношении числа образующих их электронов) с очевидностью следует:

.................................................................................(22)

Так как химические периоды системы Д.И. Менделеева состоят из тех же элементов, что и орбитальные полупериоды структурной организации электронных систем, то все сказанное в отношении последних в полной мере относится и к ним. В частности, формула (21) лишний раз подтверждает сделанный ранее вывод о взаимосвязи количества элементов в химическом периоде с номером соответствующего орбитального периода структурной организации [14]. Кроме того, выражение (17) указывает на то, что в химических периодах максимальное значение орбитального квантового числа у электронов атомов их элементов подчиняется условию:

..................................................................................... (23)

то есть орбитальное квантовое число в химических периодах принимает ряд значений . [15]

Изложенное свидетельствует, что в орбитально-волновых периодах структурной организации электронные системы атомов химических элементов обоих полупериодов дополняются одними и теми же электронами. При этом в каждом случае число электронов в s, p, d, f подгруппах сохраняет свое постоянное значение. Иначе говоря, процесс эволюции электронных систем атомов химических элементов, в пределах орбитально-волновых периодов их структурной организации, идет таким образом, что два раза подряд повторяется один и тот же набор значений и . В отношении орбитальных полупериодов и химических периодов системы Д.И. Менделеева данный факт обуславливает попарное повторение числа элементов в их пределах (14).

Попробуем объяснить это явление, для чего введем в рассмотрение понятие орбитальный номер электрона , которым будем обозначать порядковый номер электрона в подгруппе. То есть:

и, соответственно:

В излагаемом контексте можно говорить о том, что совокупность значений и описывает электронные состояния в атомах химических элементов, находящихся в пределах орбитально-волновых периодов структурной организации. При этом в каждом орбитально-волновом полупериоде разнообразие [16] электронных состояний с различными значениями и полностью исчерпывается. Возникает вопрос, почему в пределах орбитально-волновых периодов структурной организации электронных систем два раза появляются электроны с одинаковым набором значений и . Ведь, если распространить на сочетания и внутри орбитально-волновых периодов фундаментальный принцип запрета Паули, который в наиболее общей своей формулировке гласит, что “внутри атома может находиться с данным состоянием только один электрон” [17], то этого не должно быть. Можно, конечно, сказать, что никакого противоречия здесь нет, если учитывать весь набор квантовых чисел (главного, орбитального, магнитного, спинового), но тогда мы выйдем из плоскости орбитальных особенностей электронов, которые являются объектом нашего анализа. Поэтому, не выходя из указанной плоскости, будем отвечать на поставленный вопрос, проводя следующие рассуждения.

Орбитальные особенности движения электронов в атомах, помимо орбитального квантового числа, характеризуются, как известно, спиновым квантовым числом , которое отражает собственное движение электрона (вращение или спин) и принимает только два значения и , соответствующих антипараллельным направлениям вращательного движения. Значения обычно указываются противоположно направленными стрелками и , обозначающими положительное и отрицательное направления спина, соответственно. При рассмотрении электронных конфигураций атомов по умолчанию принято считать, что при данном значении сначала появляются электроны с положительным значением , а затем, когда их число достигнет величины , к ним присоединяются электроны с отрицательным значением , число которых также становится равным . Вместе с тем, ничто не мешает нам допустить (и при этом не входить ни с чем в противоречие), что в орбитально-волновых периодах структурной организации электронных систем, при данном значении , в первом полупериоде сначала появляются электроны с положительным значением , а во втором полупериоде – с отрицательным значением . То есть, если взять, например, во втором орбитальном периоде заполненные p подгруппы электронов , которые наблюдаются в первом полупериоде у неона (Ne₁₀), а во втором – у аргона (Ar₁₈), то, с учетом орбитального номера электронов , будем иметь следующие схемы распределения значений спинового квантового числа:

........................................................................................(24)

........................................................................................(25)

Сделанное допущение позволяет сформулировать (подобно принципу Паули)
орбитальный принцип запрета: в совокупности электронов, образующих орбитально-волновой период структурной организации электронных систем атомов химических элементов, при данном значении орбитального квантового числа не может быть двух электронов с одинаковым орбитальным номером и одинаковым значением спина.

Данный принцип снимает указанное противоречие и совместно со схемами (24) и (25) дает ясный ответ на поставленный вопрос относительно повторного появления в орбитально-волновых периодах электронов с одинаковым набором значений и . Соответственно, можно говорить о том, что в каждом орбитально-волновом периоде T_N два раза повторяется процесс формирования подгрупп электронов со значениями орбитального квантового числа , который идет таким образом, что электроны с одинаковыми значениями и имеют антипараллельные спины. Это обуславливает деление орбитально-волновых периодов структурной организации электронных систем на два одинаковых полупериода (зеркально-симметричных друг другу по спину образующих их электронов) и, как следствие, объясняет факт наличия в периодической системе Д.И. Менделеева периодов с одинаковым количеством химических элементов. Иначе говоря, можно утверждать, что химическая периодичность элементов периодической системы Д.И. Менделеева является вторичной по отношению к орбитальной периодичности структурной организации их электронных систем. Кроме того, принятие орбитального принципа запрета позволяет говорить о том, что одним из атрибутов общего хода эволюции электронных систем атомов химических элементов является тот факт, что появлению электронов с новым значением орбитального квантового числа предшествует реализация всего разнообразия электронных состояний, характеризуемых различными сочетаниями и при .

Литература и примечания к разд. 2

10. Таблица составлена на основе распределения электронов в атомах химических элементов, приведенного в работе: Эрдеи-Груз Т. Основы строения материи. М., 1976.

11. Граница между первым и вторым периодами по данным табл. 1 не является отчетливой и проведена по гелию на том основании, что значения R-функции электронных систем гелия и лития в плоскости электронных подоболочек (см. разд. 3) равны ? и 1,71, соответственно.

12. Работы по синтезу 118-го химического элемента в настоящее время ведутся в Объединенном институте ядерных исследований в Дубне. В случае успеха 118-й элемент планируется назвать московием (Российская газета, 30.07.2004

13. Члены этого ряда в учении о периодичности известны также как числа Ридберга.

14. Известно достаточно много способов оценки количества элементов в химических периодах системы Д.И. Менделеева. При этом практически все они делятся на две группы: эмпирические уравнения, представляющие собой специальные математические конструкции для описания априорно данного распределения элементов по периодам и двойственные по своему характеру математические выражения, принимающие тот или иной вид в зависимости от того, в четном или нечетном периоде системы Д.И. Менделеева определяется количество элементов. (См., например: Капустинский А.Ф. Формула, выражающая число элементов в периодах и начало системы Д.И. Менделеева // ДАН СССР. 1951. Т. LXXX, № 3; Клечковский В.М. Распределение атомных электронов и правило последовательного заполнения -групп. М., 1968; Трифонов Д.Н. О количественной интерпретации периодичности. М., 1971 и др.)

15. Следует отметить, что математическая форма правых частей в выражениях (15), (17), (21), (23) удивительным образом совпадает с известными формулами теории строения атома, выражающими максимальное значение орбитального квантового числа при данном главном квантовом числе n и допустимое число электронов в энергетической оболочке атома. Соответственно: (n – 1) и 2n².

16. Здесь и далее под термином разнообразие понимается число различных элементов некоторого множества. (Согласно работе: Эшби У.Р. Введение в кибернетику. М., 1959.)

17. Зоммерфельд А. Строение атома и спектры. Т. 1. М., 1956. С. 139.

Дальше

Главная страница