СИСТЕМНЫЕ ОБРАЗОВАНИЯ: ИНФОРМАЦИЯ И ОТРАЖЕНИЕ
Вяткин В.Б.
ВВЕДЕНИЕ В СИНЕРГЕТИЧЕСКУЮ ТЕОРИЮ ИНФОРМАЦИИ
Обновленное изложение теории опубликовано в "Научном журнале КубГАУ" по адресу:
http://ej.kubagro.ru/a/viewaut.asp?id=762
4.1. Отражение закрытых системных объектов
Системный
объект А, как было отмечено
выше, по значениям признака 
делится на N качественно
обособленных частей. Каждая такая
часть в условиях информационной
закрытости системного объекта (рис. 9а) является
самостоятельным системным
объектом.
Рис. 9. Отражаемый
объект A и совокупность
отражающих объектов 
а - отражаемый объект
закрыт; б - отражаемый объект открыт
Соответственно,
рассматривая отражение системного
объекта А через совокупность
его частей, с очевидностью можно
сказать, что общее количество
информации об объекте, отраженное
через эту совокупность, равно
аддитивной негэнтропии 
отражения
системных объектов, которая в
соответствии с выражениями (13) и (21)
имеет вид:
. .....................................................................................(25)
Анализ
формулы аддитивной негэнтропии
отражения (25) показывает, что
информация о системном объекте А,
отраженная через совокупность его
частей, меньше, чем самоотражаемая
им информация 
. Это говорит о
том, что отражение системного
объекта А через совокупность
системных объектов в информационном
отношении характеризуется тремя
разновидностями информации:
отражаемой, отраженной и
неотраженной. Аналитические
выражения первых двух
разновидностей информации ( и ) нам
известны. Поэтому, обозначая
неотраженную информацию символом S,
определим ее величину как разность
между отражаемой и отраженной
информациями:
.
...................................................................................................(26)
Согласно формулам (13) и (25) перепишем разность (26) в развернутом виде:
.
........................................................................(27)
Отношение 
может быть проинтерпретировано как
вероятность 
встречи
элементов, обладающих признаком 
,
среди общего числа элементов 
. В
соответствии с этим,
предварительно умножив и разделив
число под знаком второго логарифма
в выражении (27) на 
, приведем его к
виду:
.
Освобождаясь в данном выражении от знака суммы, и заменяя логарифм произведения суммой логарифмов, получаем:
=
.
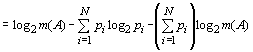Так как 
, то из последнего
выражения следует, что
окончательная формула
неотраженной информации S
имеет вид:
.
..................................................................(28)
Совместный
анализ выражений (25) и (28)
показывает, что чем более
раздробленной является система по
какому-либо признаку или, что то же
самое, чем более разнообразны и
неупорядочены ее элементы по этому
признаку, тем больше неотраженная
информация S и меньше
аддитивная негэнтропия отражения .
Иначе говоря, увеличение числа
отражающих системных объектов
приводит к возрастанию
хаотичности, неупорядоченности,
неопределенности отражения
системного образования (системы,
системного объекта), как единого
целого. То есть, чем более
неадекватно отражение, тем больше
величина неотраженной информации S.
Все это свидетельствует о том, что
неотраженная информация S
есть не что иное, как энтропия
отражения системных образований,
представленных конечным
множеством элементов.
Так как структуру системного образования, в первую очередь, характеризует количество его частей и взаимоотношение последних по числу элементов, то аддитивная негэнтропия и энтропия отражения по отношению к структуре отражаемой системы выступают в качестве показателей ее упорядоченности и хаотичности, соответственно. Чтобы лучше понять общий характер взаимоотношений аддитивной негэнтропии и энтропии отражения, приведем выражение (26) к виду:
.
.......................................................................................................(29)
Из анализа
приведенного выражения следует,
что аддитивная негэнтропия и
энтропия S отражения
являются взаимодополняющими
противоположностями и в сумме
всегда составляют постоянную
величину (при фиксированном
значении m(A)). Иначе говоря,
чтобы мы ни делали с системой, – на
сколько бы частей ее не разбивали, и
в каком бы соотношении эти части не
находились между собой по числу
элементов, сумма порядка и хаоса в
структуре системы будет сохранять
свое постоянное значение. То есть,
можно констатировать, что при любых
структурных преобразованиях
системы, происходящих без
изменения числа ее элементов, имеет
место закон
сохранения суммы хаоса и порядка:
порядок + хаос = const
При этом следует отметить, что установленный закон и его аналитическая форма (29) предсказывались философами, как “закон сохранения информации”, еще в 60-х годах прошлого столетия [33]. Вместе с тем, мы не называем выражение (29) законом сохранения информации, поскольку у автора на этот счет имеются иные, более общие соображения, которые, впрочем, в силу определенных обстоятельств, не доведены пока до уровня публикаций...
Анализируя полученные информационно-теоретические результаты, необходимо также сказать следующее. – Формула энтропии отражения закрытых системных образований (28) математически тождественна информационно-энтропийной мере К. Шеннона, взятой при двоичном основании логарифма [34], которая имеет основополагающее значение в традиционной теории информации [35]. Данный факт свидетельствует о том, что синергетическая теория информации и теория информации в версии К. Шеннона, имея предметом своего познания различные виды информации (связанной с управлением и существующей независимо от него), в то же самое время непосредственно взаимосвязаны между собой отношением взаимного проникновения друг в друга [36] и, как следствие, в своей совокупности образуют единую количественную теорию информации. Так как в наших рассуждениях энтропия отражения является вторичной, то есть выводимой через негэнтропию отражения функцией, то можно также утверждать, что в информационно-генетическом аспекте синергетическая теория информации является первичной по отношению к теории информации Шеннона.
Перейдем к
анализу поведения и
взаимоотношения аддитивной
негэнтропии и энтропии
отражения S при различном
количестве отражающих системных
объектов, а для его удобства
перепишем выражение (29) в
развернутом виде:
.
Рассмотрим
сначала два противоположных
процесса: когда 
и 
.
В первом
случае, при и
соответствующем 
, происходит
увеличение аддитивной негэнтропии и
уменьшение энтропии S, что в пределе,
когда N = 1, дает:
и S
= 0. Во
втором случае, когда и 
, наблюдается
обратное движение, то есть,
увеличивается энтропия S и уменьшается
негэнтропия . Соответственно
получаем, что при 
и 
негэнтропия достигает своего
минимального значения. Так как в
проводимых рассуждениях
количество элементов не является
фиксированной величиной, то
определим точную нижнюю грань
аддитивной негэнтропии отражения
закрытого системного объекта для
всего множества возможных значений
, то есть, когда 
. В
соответствии с формулой
негэнтропии 
(21) имеем:
[37]
Полученный результат по своей математической форме соответствует общепринятой единице измерения количества информации – биту, но его содержательная сущность принципиально отличается при этом от понимания бита в традиционной теории информации, где 1 бит интерпретируется как максимальное количество информации, которое можно получить в результате выбора одной из двух возможностей. В связи с этим уточним, что следует понимать под единицей измерения информации при количественном определении того ее вида, который существует независимо от управления. Дадим такой единице название бит отражения и определим ее следующим образом: 1 бит отражения есть минимальное количество информации о системном образовании, которое может быть отражено через совокупность его частей.
Рассмотрим
теперь особенности
взаимоотношений энтропии S и
аддитивной негэнтропии при
фиксированном и различном N.
При этом сначала определим их
значения, соответствующие
максимальной хаотичности или
минимальной упорядоченности
отражения при данном N.
Хаотичность отражения системного образования является максимальной, когда все его качественно обособленные части представлены одинаковым числом элементов или, что, то же самое, все отражающие признаки представляют собой равновероятные события. Соответственно, непосредственно из формулы (28) получаем максимальное значение энтропии отражения:
.
............................................................................(30)
С учетом этого из выражения (29) следует минимальное значение аддитивной негэнтропии отражения:
.
......................................................................(31)
Максимальная
упорядоченность отражения
системных образований при данном N,
в свою очередь, будет иметь место,
когда количество элементов в одной
части, согласно (24), будет равно 
, а
все остальные части будут включать
в себя только по 2 элемента.
Соответственно, максимальное
значение аддитивной негэнтропии и
минимальное значение энтропии,
согласно выражениям (25) и (28), будут
равны:
....................................................(32)
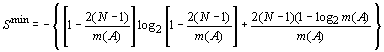....................................................(33)
Построим
графики 
, как функций от N
при фиксированном и проведем анализ
полученной диаграммы (рис.10).
Рис. 10. Информационное
поле отражения системных объектов
Приведенные
графики изначально образуют 2
контура: энтропийный abdefh и негэнтропийный
или информационный cdfghb, которые
локализуют соответствующие
области всех возможных значений
энтропии и аддитивной негэнтропии
отражения закрытых системных
объектов при данном и произвольных
значениях N и 
. Пересечение этих
контуров по точкам b и f позволяет
выделить 3 интервала значений N
(левый, центральный и правый) с
присущими каждому интервалу
особенностями взаимоотношения S и
, определяющими в целом
характер структурного отражения
системных образований. Определим
границы этих интервалов и
рассмотрим соответствующие им
особенности отражения.
В точке b 
, то есть, согласно (30) и
(31), имеем, что 
, откуда 
. В
точке f 
и графическое
решение уравнения, образованного
правыми частями выражений (32) и (33)
дает, что 
. При этом необходимо
отметить, что поскольку N может принимать
только целочисленные значения, то
отмеченные границы интервалов
практически определяются с
точностью до ближнего большего
целого.
Отражение
системных образований, попадающих
в левый интервал 
, характеризуется
тем, что при любых соотношениях их
частей между собой по количеству
элементов, справедливо неравенство
, то есть
упорядоченность отражения
превосходит его хаотичность.
В правом
интервале 
наблюдается
противоположная картина, когда при
любых условиях имеет место
неравенство 
, что
соответствует погашению
отражаемой информации и
преобладанию хаоса над порядком.
В
центральном интервале 
происходит
пересечение областей возможных
значений аддитивной негэнтропии и
энтропии S, вследствие чего
между ними здесь наблюдаются
различные взаимоотношения. В общем
случае и S могут быть как
больше, так и меньше друг друга, но в
ряде случаев, соответствующих
прямолинейной области между
точками b и f , имеет место их
равенство между собой. В
содержательном плане можно
говорить, что в интервале значений N
от 
до 
в отражении
системных объектов наблюдается
тенденция к взаимному
уравновешиванию порядка и хаоса и
может достигаться
негэнтропийно-энтропийное
(информационно-энтропийное)
равновесие, когда отражение
системного объекта является
насколько хаотичным настолько и
упорядоченным.
Отмеченные
особенности отражения позволяют
все системные образования
классифицировать, в зависимости от
числа их качественно обособленных
частей и вида соотношения
аддитивной негэнтропии
и энтропии S,
на 5 типов:
-
упорядоченные: 
;
-
хаотично-упорядоченные: 
;
-
равновесные: 
;
-
упорядоченно-хаотичные: 
;
- хаотичные:
.
Кроме приведенной классификации любые системные образования, с позиций закона сохранения суммы хаоса и порядка (29), можно сопоставлять между собой по величине отношения порядка к хаосу, которое будем называть R-функцией [38]:
.
................................................................................................(34)
Количество
качественно обособленных частей и
их соотношение между собой по числу
элементов определяют в целом
структурную организацию системных
образований, а аддитивная
негэнтропия и энтропия
отражения S являются мерами
ее упорядоченности и хаотичности.
То есть R-функция представляет
собой обобщенную
информационно-энтропийную
характеристику
структурированности системных
образований, значение которой
говорит о том, что и в какой мере
преобладает в их структурной
организации: порядок (негэнтропия)
или хаос (энтропия). Так, если R > 1, то в структурной
организации преобладает порядок, в
противном случае, когда R
< 1 - хаос.
При R = 1 хаос и порядок
уравновешивают друг друга, и
структурная организация системных
образований является равновесной.
Наглядной иллюстрацией изменения
значений R-функции (а также
изменения и S), в зависимости от
того, на сколько частей разделяется
системное образование, является
рис. 11, на котором приведено
последовательное деление системы,
состоящей из 16 элементов, на N =
2, 4, 8, 16 равновеликих частей.
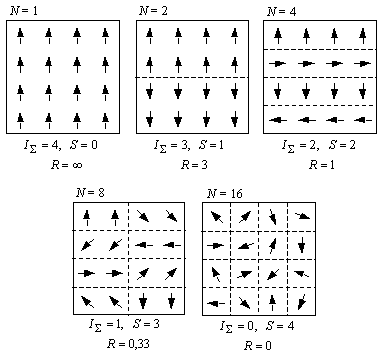
Рис. 11. Значения функций
порядка (), хаоса (S) и
структурной организации (R)
системы,
состоящей из 16-ти элементов, при
различном числе (N) ее
равновеликих частей
Для лучшего восприятия описанных информационно-энтропийных особенностей отражения закрытых системных образований целесообразно в популярной форме, на конкретных примерах, показать, что значит структурный хаос правого интервала и порядок левого, а также их уравновешивание друг друга в центральном интервале значений N. Обратимся за примерами к структурной лингвистике, к которой традиционно обращаются при популяризации теории информации и возьмем обезьяну, с которой “работал” французский математик Э.Борель [39]. Проводя мысленный эксперимент, посадим обезьяну за пишущую машинку. Обезьяна, случайным образом ударяя по клавишам, получает чехарду букв, лишенную всякого смысла. Такой “текст” олицетворяет хаос правого интервала, а его R-функция стремится к нулю (при длине “текста”, не превышающем количество букв используемого алфавита). Посадим теперь за другую пишущую машинку дятла, который, методично ударяя по одной и той же клавише, иногда даже “случайно промахиваясь”, выдает практически однобуквенную последовательность. “Текст” дятла также является совершенно бессодержательным и соответствует крайней левой части левого интервала, где идеальный порядок и серое однообразие. R-функция при этом стремится к бесконечности. Продолжая лингвистическую тему, в качестве примера гармонии отношений хаоса и порядка, присущей информационно-энтропийному равновесию центрального интервала, приведем поэму А.С.Пушкина “Евгений Онегин”, в которой структурная организация логически завершенных участков текста выглядит следующим образом: первое четырнадцатистишие – R = 0,94; второе четырнадцатистишие – R = 0,98; и т.д. В качестве же эталона систем, структурная организация которых обладает устойчивой гармонией отношений хаоса и порядка, укажем семейство систем натурального ряда. При этом под системой натурального ряда понимается система, соотношение частей которой по количеству элементов выражается натуральным рядом чисел или, иначе говоря, числу элементов в части соответствует ее порядковый номер. Например, выражение: “N-я система натурального ряда”, говорит о том, что в структуре системы выделяется N частей, в первой из которых содержится 1 элемент, во второй – 2 элемента, …, в N-й – N элементов. График на рис. 12 показывает, что R-функция систем натурального ряда, при последовательном увеличении N, монотонно возрастает и асимптотически приближается к единице.
Рис. 12. График R-функции систем натурального ряда чисел
Литература и примечание к разд. 4.1
33. Например, И.Б. Новик в 1962 г. предложил трактовать информацию как форму отражения и считать, что информация – это упорядоченность отражения, а шум – неупорядоченность, хаотичность отражения. При этом было сделано предположение о потенциальном существовании закона сохранения информации (количества отражения) в закрытой системе, который должен иметь следующую форму: I + N = const, где I – количество информации, а N – количество шума. Эти рассуждения, по-видимому, можно считать предсказанием выражения (29). (См.: Новик И.Б. Негэнтропия и количество информации // Вопросы философии, 1962, № 6.)
34. Следует отметить, что формула Шеннона получена нами без каких-либо допущений относительно вида энтропии отражения, в то время как сам Шеннон руководствовался априорными требованиями к свойствам своей информационно-энтропийной меры. При этом использование логарифмической функции обосновывалось соображениями ее технического удобства, а основание логарифма предлагалось выбирать в зависимости от используемых единиц информации: двоичная единица (бит) – двоичный логарифм, десятичная единица (дит) – десятичный логарифм, натуральная единица (нат) – натуральный логарифм. (См.: Шеннон К. Указ. соч.)
35. Заметим, что в отношении подобного рода совпадений математических формул, выражающих различные сущности, признанный авторитет в области теории информации – академик А.Н. Колмогоров, писал: “Такие математические аналогии следует всегда подчеркивать, так как сосредоточение на них внимания содействует прогрессу науки”. (Колмогоров А.Н. Указ. соч. С. 39.).
36. Это является подтверждением философского заключения Урсула А.Д. о взаимоотношениях различных видов информации: “В природе, по-видимому, нет резких граней … между различными видами самой информации. Высшие виды информации “незаметно” переходят в низшие, и связь с управлением отнюдь не служит той границей, за которой уже нет информации”. (Урсул А.Д. Указ. соч. 1975. С. 62. (Разрядка моя – В.В.))
37.
Примечательно, что в том случае,
когда N = m(A) и познавательной
ситуацией диктуется необходимость
получения отличных от нуля
значений негэнтропии 
(см. разд. 3),
минимальное значение аддитивной
негэнтропии отражения закрытого
системного объекта, независимо от
величины m(A), также составляет 1
бит.
38. Название функции дано по первой букве английского слова reflection, что в переводе на русский язык означает отражение.
39. См.: Пригожин И., Стенгерс И. Время, хаос, квант. М.: Прогресс, 1994.
