СИСТЕМНЫЕ ОБРАЗОВАНИЯ: ИНФОРМАЦИЯ И ОТРАЖЕНИЕ

Вяткин В.Б.

ВВЕДЕНИЕ В СИНЕРГЕТИЧЕСКУЮ ТЕОРИЮ ИНФОРМАЦИИ

Обновленное изложение теории опубликовано в "Научном журнале КубГАУ" по адресу:

http://ej.kubagro.ru/a/viewaut.asp?id=762

2. Синергетический подход к количественному
определению информации

Ставя перед собой цель, – получение формулы негэнтропии отражения системных объектов и, сознавая, что эта цель не может быть достигнута с помощью традиционных мер информации, необходимо, прежде всего, ответить на два вопроса: что следует в данном случае понимать под термином “информация” и что принимать за ее количественную характеристику.

Отвечая на первый вопрос, будем исходить из общеупотребительного и наиболее простого определения информации как сведений о чем-либо, и учитывая, что любой системный объект рассматривается нами как единое целостное образование, конкретизируем это определение информации в наших исследованиях как сведения о системном объекте как едином целом. В основу же ответа на второй из поставленных вопросов положим очевидное утверждение, что наиболее полную и адекватную информацию о произвольном системном объекте А непосредственно отражает (самоотражает) сам системный объект А. При этом, в контексте оценки негэнтропии отражения , отметим, что при наличии равенства отражение системных объектов A и B друг через друга не отличается от их отражения через самих себя (рис. 1 д). Это позволяет говорить о том, что количественная сторона, как негэнтропии отражения системных объектов, так и информации, самоотражаемой системными объектами, имеет одну и ту же природу. С учетом сделанных замечаний в качестве ответа на второй вопрос определим количество информации , которое системный объект А отражает о самом себе как едином целом.

Прежде всего отметим, что о системном объекте А нам априорно известно только то, что его элементы обладают некоторым отличительным признаком , а их общее число равно . При этом отчетливо осознается, что если даны, например, два системных объекта с различным числом элементов, то большее количество информации о самом себе, как едином целом, будет отражать тот из системных объектов, в составе которого находится большее число элементов. Короче говоря, представляется очевидным, что информация , самоотражаемая системным объектом А, должна быть монотонно возрастающей функцией от . В соответствии с этим принимается информационная аксиома: для любых двух системных объектов А и В, таких, что , имеет место неравенство:

...................................................................................................................(1)

При этом, в качестве дополнительного аргумента в пользу принятой аксиомы, укажем тот факт, что монотонный характер информационных мер априорно принимался и при разработке традиционной теории информации [27].

Является очевидным, что системный объект А и любой элемент соотносятся между собой как целое и его одноэлементная часть. Такое соотношение, рассматриваемое с диалектических позиций, обуславливает два существенных момента.

Во-первых, понятие целое, по определению [28], атрибутивно связано с совокупностью элементов отдельно взятого объекта, и потому системный объект A не может состоять только из одного элемента, то есть:

...............................................................................................................(2)

При этом отметим, что в противном случае, если в составе некоторой системы по какому-либо отличительному признаку будет выделяться единичное множество элементов , то будем называть такое множество квазисистемным объектом.

Во-вторых, совокупность элементов, составляющих системный объект A, представляет собой не механическое собрание предметов, обладающих признаком P_A и существующих независимо друг от друга, а единое целостное образование, в составе которого элементы обладают интегративными характеристиками, не присущими им в их разобщенном виде. Иначе говоря, показателем системного объекта, как единого целого, являются интегративные характеристики его элементов, и соответственно, наличие у этих характеристик какого-либо числового параметра, зависящего от общего числа элементов, может служить основой для получения формулы самоотражаемой информации.

В соответствии со сказанным в качестве интегративной характеристики элементов системного объекта А принимается поставленный им в соответствие индивидуальный символьный код, составленный с помощью какого-либо n-символьного алфавита, длина которого (число символов кода) функционально взаимосвязана с общим числом элементов . Чтобы выяснить характер зависимости от рассмотрим процесс увеличения числа элементов , представив его в виде роста ориентированного дерева, совокупность висячих вершин которого взаимно-однозначно соответствует множеству элементов , а максимальное число дуг, выходящих из одной вершины, равно числу символов (n) алфавита, выбранного для составления интегративных кодов. При этом каждой из смежных дуг, в алфавитном порядке, ставится в соответствие свой символ и, как следствие, в качестве индивидуального интегративного кода какого-либо элемента выступает последовательность символов, находящихся на пути движения из начальной вершины дерева в соответствующую данному элементу висячую вершину. Модель такого дерева (которое будем называть деревом кодов) при n = 2 и использовании в качестве алфавита упорядоченной пары символов <0,1> приведен на рис. 3.

Рис. 3. Модель дерева кодов при n = 2

Анализ представленной модели дерева кодов показывает, что в общем случае все множество элементов системного объекта A по длине интегративных кодов разбивается на два подмножества и , таких, что:

, ................................................................................................(3)

где - целочисленная часть .

Так как длина интегративного кода элементов согласно выражению (3) не является постоянной величиной и может принимать два значения, то в дальнейшем будем рассматривать среднюю длину кода , которая является однозначной функцией от и в общем случае имеет вид:

. ..........................................................................................(4)

Определим величину при различных значениях n и начнем со случая, когда n = 2.

Анализируя рис. 3, нетрудно видеть, что при n = 2 возрастание числа элементов системного объекта A на единицу обуславливает уменьшение на единицу числа элементов с длиной кода x и увеличение числа элементов с длиной кода (x + 1) на два элемента, то есть:

Учитывая это, для определения и при n = 2, составим систему уравнений:

,

разрешая которую, получаем:

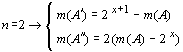. .......................................................................................(5)

Подставляя значения и из (5) в (4) и, проводя несложные преобразования, приходим к следующему значению средней длины интегративного кода элементов составленного с помощью двоичного алфавита:

. ......................................................................................(6)

Рассмотрим теперь ситуацию когда n > 2, пример которой, для случая n = 3, представлен на рис. 4.

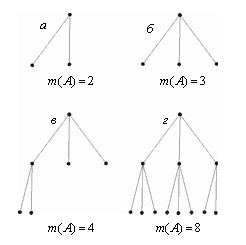
Рис. 4. Деревья кодов при n = 3

Из анализа рисунка видно, что характер изменения значений и при последовательном возрастании на единицу, в отличие от случая, когда n = 2, не является постоянным. – Пока (рис. 4а,б) наблюдается равенство а . После того, как начальная вершина дерева насыщается по количеству выходящих из нее дуг, начинается последовательное насыщение выходящими дугами висячих вершин (рис.4в). При этом, при переходе от одной висячей вершины к другой, повторяется один и тот же процесс: сначала скачком увеличивается на два элемента, а уменьшается на один элемент, после чего (до насыщения вершины) последовательно увеличивается на единицу, а сохраняет свое постоянное значение. Учитывая, что при насыщении последней из вершин (длина пути в которые равна x) становится равным нулю (рис.4 г), в первом приближении рост кодового дерева при n > 2 можно представить следующим образом:

.....................................................(7)

Соответственно, из совместного анализа выражения (7) и рис.4, следует, что величина , при n > 2 принимает следующие значения:

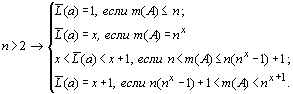.........................................................................(8)

Проводя теперь анализ выражений (6) и (8), с позиций информационной аксиомы (1) можно сказать следующее. Средняя длина интегративного кода элементов при n = 2 является однозначной функцией от , а её замена на в выражении (6) не противоречит информационной аксиоме (1). Например, если нам даны два системных объекта А и В, такие, что m(A) = 2, а m(B) = 3, то, согласно выражению (6), мы получаем следующие значения самоотражаемой информации: , и, соответственно, имеем согласие с аксиомой (1), поскольку 1,67 >1. Такая же замена на в выражении (8), при выполнении первого и четвертого условий, входит в противоречие с аксиомой (1). Например, при n = 3, в условиях предыдущего примера, будем иметь, что и, соответственно, аксиоматическое требование (1) не выполняется. Из сказанного следует принципиально важный для нас методологический вывод: средняя длина интегративного кода элементов системного объекта находится во взаимно-однозначном соответствии с общим числом его элементов только тогда, когда интегративный код составлен с помощью двоичного алфавита.

Таким образом, мы пришли к тому, что количество информации , отражаемой системным объектом А о самом себе, как едином целом, равно:

. ............................................................................................(9)

Нетрудно видеть, что, если , то . В том же случае, когда наблюдается неравенство , что иллюстрируют графики зависимости и от , представленные на рис. 5.

Рис. 5. Графики функций I_A и

Определим теперь точную верхнюю грань отклонения от как величину

. .........................................................................................(10)

Применяя необходимое условие экстремума, и, полагая, что , x = const, приходим к уравнению:

,

которое, после дифференцирования по , приобретает вид:

и после несложных преобразований имеет своим решением

. ..................................................................................................(11)

Подставляя значение из (11) в разность и, представляя при этом информацию в развернутом виде согласно (9), имеем:

Так как в соответствии со свойствами логарифмов , то из последнего выражения окончательно получаем, что отклонение значений информации от ограничено постоянной величиной:

что наглядно иллюстрирует рис. 6.

Рис. 6. График разности I_A -

Значение полученной постоянной позволяет сделать следующее приближение:

. .............................................................................(12)

Относительная погрешность такого приближения равна:

,

а характер ее изменения, в зависимости от величины , показан на рис. 7.

Рис. 7. График зависимости E(IA) от m(A)

Так как , а является монотонно возрастающей функцией от , значения которой удовлетворяют информационной аксиоме (1), то, учитывая выражение (12), в практическом отношении принимается эквивалентность:

................................................................................................(13)

Таким образом, можно констатировать, что в настоящем разделе мы получили новый подход к количественному определению информации, основанный на совместном и одновременном учете всех элементов системного объекта, без индивидуального выделения какого-либо из них в качестве случайного события, результата испытания и т.п. То есть мы ушли от традиционного увязывания количества информации с результатами выбора одной из множества различных возможностей. Вместе с тем, следует отметить, что форма выражения самоотражаемой информации в формуле (13) является математическим подобием информационной меры Хартли [29], взятой при единичном выборе и двоичном основании логарифма, но принципиально отличается от нее тем, что количество символов используемого алфавита в мере Хартли является числом логарифма, а в выражении (13) – его основанием. Данный факт позволяет говорить о том, что между разработанным подходом к определению количества информации и комбинаторным направлением традиционной теории информации существует определенная взаимосвязь.

Определяясь теперь с тем, как следует назвать разработанный подход к количественному определению информации, будем исходить из структуры выражений (9) и (13), из которых следует, что количество информации , отражаемое системным объектом A о самом себе как едином целом, является результатом совместного отражающего действия всей совокупности элементов . Поэтому дадим новому подходу название – синергетический, учитывая при этом тот факт, что термин синергетика буквально означает совместный, согласованно действующий. Соответственно, интегральную совокупность информационно-теоретических результатов, полученных на его основе, будем называть синергетической теорией информации.

Перейдем теперь, основываясь на синергетическом подходе к количественному определению информации, и одновременно развивая его, к решению задачи по оценке негэнтропии отражения системных объектов, поставленной в разд. 1.

Литература и примечания к разд. 2

27. Например, К. Шеннон во введении своей знаменитой статьи “Математическая теория связи” (1948) писал: “Если множество сообщений конечно, то число сообщений или любую монотонную функцию от этого числа можно рассматривать как меру информации, создаваемой выбором одного сообщения из этого множества …” (Шеннон К. Указ. соч. С. 244).

28. Философский энциклопедический словарь. М.: Сов. Энциклопедия, 1983.

29. Напомним, что Хартли (Хартли Р.В.Л. Указ. соч.), решая задачу сравнения пропускной способности различных систем технической связи, предложил считать передаваемую информацию пропорциональной числу выборов, которые необходимо осуществить для передачи сообщения с помощью n-символьного алфавита. Полученная им информационно-количественная мера H, имеет вид: , где: n - число символов используемого алфавита, а m - количество выборов, которые необходимо осуществить, чтобы передать заранее известное сообщение по каналу технической связи. При этом основание логарифма было предложено считать произвольным.

Дальше

Главная страница