СИСТЕМНЫЕ ОБРАЗОВАНИЯ: ИНФОРМАЦИЯ И ОТРАЖЕНИЕ
Вяткин В.Б.
ЗАДАЧА
ОЦЕНКИ НЕГЭНТРОПИИ ОТРАЖЕНИЯ
СИСТЕМНЫХ ОБЪЕКТОВ
И ТРАДИЦИОННЫЕ ПОДХОДЫ К
КОЛИЧЕСТВЕННОМУ
ОПРЕДЕЛЕНИЮ ИНФОРМАЦИИ
(Материалы из
диссертации: Вяткин В.Б. Математические
модели
информационной оценки признаков
рудных объектов)
.....................................................................................................................................
Вероятностный
подход к количественному
определению информации
Наиболее известным и широко применяемым на практике является вероятностный подход к измерению информации. На основе этого подхода разработан обширный раздел количественной теории информации, называемый также по имени его основоположника, как "теория информации Шеннона". Главной отличительной особенностью вероятностного подхода от комбинаторного является тот факт, что он основан на вероятностных допущениях относительно пребывания какой-либо системы в различных состояниях. При этом общее число элементов (микросостояний, событий) системы не учитывается. За количество информации здесь принимается снятая неопределенность выбора из множества возможностей, имеющих, в общем случае, различную вероятность.
Основополагающая роль в вероятностном подходе принадлежит энтропии множества вероятностей, формула которой была получена в 1948 году американским исследователем К. Шенноном. Предлагая для измерения количества информации свою знаменитую энтропийную меру, К. Шеннон руководствовался следующими соображениями.
"Предположим,
что имеется некоторое множество
возможных событий, вероятности
осуществления которых суть 
. Эти
вероятности известны, но это – все,
что нам известно относительно того,
какое событие произойдет. Можно ли
найти меру того, насколько велик
"выбор" из такого набора
событий или сколь неопределенен
для нас его исход?" [25, с. 259].
Для такой меры Н выдвигается требование: она должна обладать следующими тремя свойствами.
1. Н
должна быть непрерывной
относительно 
.
2. Если все равны,
то Н должна быть монотонно
возрастающей функцией от n.
3. Если выбор распадается на два последовательных выбора, то первоначальная Н должна быть взвешенной суммой индивидуальных значений Н каждого из выборов.
Последнее
свойство поясняется рисунком 3, где
показаны две ситуации выбора из
трех возможностей, имеющих
вероятности 
. В левой ситуации
выбор любой возможности является
однократным, а в правой ситуации в
двух случаях из трех необходимо
предварительно сделать
соответствующий дополнительный
выбор из двух равновероятных
возможностей.
Рис. 3. Выбор из трех возможностей
Согласно третьему свойству в левой и правой ситуациях значения Н должны быть одинаковы, что выражается следующим образом:
,
где коэффициент 1/2 является весовым множителем, указывающим, что второй выбор выполняется только в половине случаев.
В процессе последующих исследований К. Шеннон доказал теорему: "Существует единственная функция Н, удовлетворяющая трем перечисленным выше свойствам. При этом Н имеет вид:
,
...............................................................(16)
где К – некоторая положительная постоянная" [25, с. 260].
Форма полученной функции Н проявила определенную степень подобия с термодинамической энтропией Больцмана, на основании чего и по совету Дж. Неймана [15] Шеннон назвал функцию Н энтропией множества вероятностей (см. примечание 1), утверждая при этом, что "она является разумной количественной мерой возможности выбора или мерой количества информации" [25, с. 262].
Нетрудно видеть, что в том случае, когда все вероятности равны между собой, информационная мера Шеннона сводится к двоичному логарифму Хартли от числа возможностей:
Последнее свидетельствует о том, что во взаимоотношениях вероятностного и комбинаторного подходов соблюдается принцип соответствия, согласно которому "новая теория, претендующая на более широкую область применимости, чем старая, должна включать последнюю как предельный случай" [18, с. 1257].
Отметим, что
на основании
информационно-энтропийной меры (16) содержательно
оформилась и единица измерения
количества информации, имеющая
название "бит" (термин,
предложенный Тьюки [25]). Причем в
математическом отношении 
, а в
содержательной
информационно-вероятностной
интерпретации, исходя из того, что
при 
имеет место
неравенство 
, 1бит представляет
собой максимальную энтропию выбора
из двух возможностей. Менее
строгим, но более распространенным,
является понимание бита, как
максимального количества
информации, которое можно получить
при ответе на вопрос в форме
"да" - "нет".
Математический
аппарат теории информации в версии
Шеннона, основанный на функции (16), в
настоящее время является весьма
разработанным и разветвленным. Мы
не будем заниматься его детальной
характеристикой, поскольку в его
рамках, главным образом,
рассматриваются неразрывно
связанные между собой совокупности
событий (символов, элементов,
состояний системы и т.п.). (Неразрывность
обусловлена тем, что 
) В отношении
информационно-количественной
оценки системных объектов это
означает, что речь идет о
характеристике совокупности
отражающих объектов в целом. Нас же
сейчас интересует негэнтропийная
оценка индивидуальной взаимосвязи
отражаемого объекта с каким-либо
отражающим объектом. Поэтому
остановимся только на тех моментах
теории Шеннона, которые имеют к
этому отношение. Таких моментов в
сущности два, и они связаны с
так называемой частной
информацией, содержащейся в
отдельных событиях. Покажем эти
моменты согласно работе Е.С.
Вентцель [4].
Первое.
Формула Шеннона может быть
представлена как математическое
ожидание величины 
:
,
откуда
частная информация 
, получаемая от
отдельного события, состоящего в
том, что некоторая система Х находится
в состоянии 
i имеет вид:
.................................................................. (17)
Второе. Когда
рассматриваются две
взаимосвязанные системы Х и Y,
частная информация 
, содержащаяся в
событии 
относительно системы Х, выражается
следующим образом:
,
.............................................(18)
где 
-
условная вероятность 
при наступлении .
Из анализа
структуры выражения (18) выводится
частная информация 
о событии , содержащаяся
в событии :
.......................................................
(19)
Частная
информация имеет название
"информация от события к
событию" и интерпретируется
следующим образом: "Частная
информация о событии, получаемая в
результате сообщения о другом
событии, равна логарифму отношения
вероятности первого события после
сообщения к его же вероятности до
сообщения" [4, с. 492].
Нетрудно видеть, что информация от события к событию может иметь как положительные, так и отрицательные значения, то есть:
и 
.
Приведенная характеристика вероятностного подхода к определению количества информации относится к дискретным средам. Так как по существующим представлениям любая непрерывная среда может быть представлена в дискретном виде, покажем вероятностный подход к измерению информации для случая непрерывных сред, разработанный одним из основоположников кибернетики Н. Винером [5]. (В отношении же квантования непрерывных сред можно привести мнение академика В.М. Глушкова, связанное с кибернетическими системами: "Всякий реальный преобразователь непрерывной информации обладает по крайней мере тремя ограничениями, делающими возможным дискретный подход к описанию его работы" [8, с. 40]. Такими ограничениями являются разрешающая способность, чувствительность и пропускная способность преобразователя. )
Н. Винер исходил из того, что в кибернетических системах элементарной формой информации является запись (запоминание) выбора одной из двух равновероятных возможностей, который он называл решением. Если известно, что значение некоторой непрерывной величины находится внутри интервала (0, 1) и стоит задача совершенно точно определить это значение, то количество выборов, которое необходимо при этом сделать, выражается бесконечной двоичной дробью:
где 
имеет значение 0 или 1.
В
действительности никакое
измерение непрерывной величины не
может быть совершенно точным, в
связи с чем далее Н. Винер рассуждал
следующим образом: "Если
измерение имеет равномерно
распределенную ошибку, лежащую в
интервале длины 
, где 
есть первый
разряд, не равный 0, то, очевидно, все
решения от 
до 
и, возможно, до 
будут значащими, а все последующие
нет. Число принятых решений,
очевидно, близко
. .............................................................(19)
Мы примем это выражение за точную формулу количества информации и за его определение" [5, с. 82].
Выражение (19) имеет следующую авторскую интерпретацию: "Мы знаем априори, что некоторая переменная лежит между нулем и единицей, и знаем апостериори, что она лежит в интервале (a,b) внутри интервала (0,1). Тогда количество информации (I), полученное нами из апостериорного знания, равно" [5, с. 83]:
..................................................
(20)
В том случае,
когда априорно известно, что
вероятность нахождения
определяемой величины между x и
равна 
, а апостериорная
вероятность равна 
, Н. Винером
предложено для оценки информации,
которую дает апостериорная
вероятность, использовать формулу:
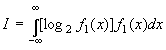......................................................... (21)
Нетрудно видеть, что при квантовании интервалов каким-либо образом формулы Винера (20) и (21) сводятся соответственно к двоичному логарифму Хартли и энтропии Шеннона. Причем в последнем случае тот факт, что в формуле Шеннона имеется отрицательный множитель (–1), а в формуле Винера его нет, принципиального значения не имеет. Это наглядно показал Р.Эшби на примере двух способов измерения расстояний с помощью линейки [26]. Приведем этот пример.
На рис. 4
показаны две линейки W и S (W и S – начальные
буквы фамилий Винер и Шеннон на
английском языке). Даны две точки P и Q,
соответствующие состояниям
неопределенности до (Р) и после (Q)
получения сообщений. Естественно,
что количество информации,
получаемое в результате сообщения,
равно расстоянию PQ, которое может
быть измерено двумя эквивалентными
способами.
Рис. 4. Измерение
расстояния между точками P и Q
с помощью
двух линеек W и S.
По способу Винера линейка W прикладывается к точкам P и Q произвольным образом, а расстояние PQ определяется как разность отсчетов: (отсчет для Q) минус (отсчет для Р). По способу Шеннона линейка S прикладывается строго определенным образом, а именно – нуль совмещается с точкой Q и тогда расстояние PQ определяется как: минус (отсчет для Р). То есть принципиального различия в измерении количества информации по способам Винера и Шеннона не существует.
В заключение общей характеристики вероятностного подхода отметим, что его развитие отодвинуло в тень чисто комбинаторный подход определения количества информации, за внешней простотой которого, в соответствии с мнением А.Н. Колмогорова [12], потенциально скрываются нетривиальные решения различных информационных проблем.
Анализ приведенных сведений о вероятностном подходе к количественному определению информации позволяет высказать следующее.
Основополагающая
формула вероятностного подхода –
формула Шеннона (16) – в
рассматриваемом аспекте
изначально имеет интеграционную
природу относительно n-й совокупности
отражающих объектов закрытого
системного объекта, в силу чего,
"вклад" i-го отражающего
объекта в получаемое количество
информации по этой формуле, не
может рассматриваться в качестве
его негэнтропийной оценки. Это
также следует из того, что,
например, если мы имеем два
отражающих системных объекта B и
C с вероятностями
встречи их существенных признаков 
и 
у
элементов отражаемого объекта,
соответственно равными 
и 
, то, оценивая
"вклад" каждого из них в общее
количество информации по формуле
Шеннона, как величину 
, мы получим, что
эти "вклады" равны:
,
чего, естественно, при оценке негэнтропии отражения быть не должно.
Формула частной информации, выражаемая логарифмом вероятности (17), в данном случае дает нам, что
,
то есть мы опять получаем выше рассмотренное приложение формулы Бриллюэна (14).
В отношении же частной информации "от события к событию" (19) можно сказать, что уже сама констатация того, что эта информация может принимать отрицательные значения, вызывает принципиальные возражения против ее использования для количественной оценки негэнтропии отражения системных объектов, поскольку последняя является неотрицательной величиной. В связи с этим следует отметить, что практическое использование информации "от события к событию" ограничено только тем числом случаев, когда познающего субъекта интересует количественный аспект прагматической ценности получаемых сведений. То есть, если полученная информация приближает субъекта к достижению некоторой утилитарной цели, то ее количественная оценка по формуле (19) является положительной, а если она отдаляет от достижения цели, то и оценка ее отрицательна. Проиллюстрируем это классическим примером, взятым из работы Е.А. Вентцель. – "В урне 3 белых и 4 черных шара. Из урны вынуто 4 шара, три из них оказались черными, а один – белым. Определить информацию, заключенную в наблюденном событии B по отношению к событию A - следующий вынутый из урны шар будет черным" [4, с. 493]. Решение по формуле (19) дает, что
В приведенном примере негэнтропия отражения представляет собой информацию, которую отражает группа шаров одного цвета (белого или черного) относительно всей совокупности шаров, находящихся в урне, то есть она никакого отношения к информации "от события к событию" не имеет.
Изложенное свидетельствует, что вероятностный подход к определению количества информации, основанный на формуле Шеннона (16), не дает удовлетворительных способов оценки негэнтропии отражения системных объектов. В связи с этим уместно привести высказывание математика Р.Л. Добрушина относительно теории Шеннона в целом: "Столь общий многообразный объект, как информация, не может допускать единого метода численного измерения, а идеи Шеннона обоснованы лишь в применении к той важной, но все же ограниченной ситуации, когда рассматриваются оптимальные методы кодирования и декодирования информации в целях передачи ее по каналам связи или ее хранения" [10, с. 254]. Примечательно, что сам Шеннон, понимавший ограниченность сферы приложения вероятностной теории информации, писал: “Сознавая, что теория информации является сильным средством решения проблем теории связи, нельзя забывать, что она не является панацеей для инженера-связиста, а тем более для представителей всех других специальностей” [25, с. 667] .
Примечания
Примечание 1. Называя функцию Н "энтропия множества вероятностей", Шеннон комментировал это следующим образом: "Меня больше всего беспокоило, как назвать эту величину. Я думал назвать ее "информацией", но это слово слишком перегружено, поэтому я решил остановиться на "неопределенности". Когда я обсуждал все это с Джоном фон Нейманом, тот предложил лучшую идею. Фон Нейман сказал мне: "Вам следует назвать ее энтропией по двум причинам. Во-первых, ваша функция неопределенности использовалась в статистической механике под этим названием, так что у нее уже есть имя. Во-вторых, и это важнее, никто не знает, что же такое эта энтропия на самом деле, поэтому в споре преимущество всегда будет на вашей стороне". (Цит. по кн.: Мещеряков А.С., Улыбин С.А. Термодинамика. Феноменологическая термомеханика. М.: Химия, 1994. С. 257.)
