СИСТЕМНЫЕ ОБРАЗОВАНИЯ: ИНФОРМАЦИЯ И ОТРАЖЕНИЕ

Оганов В.В. Доклад «Периодический закон Менделеева в свете синергетической теории информации» на Всероссийском научном форуме молодежи «Шаг в будущее» (Москва, 19-23 марта 2012г.)
Режим доступа: http://www.mgdvorec.ru/about/structure/ott/news 
 

 
Вяткин В.Б. Периодический закон
Д.И. Менделеева в свете синергетической теории информации // Энергоанализ и энергоэффективность – 2004, № 1(2) – с.30-33.
Режим доступа: http://vbvvbv.narod.ru/Mendeleev_STI/Mendeleev2004.pdf

1 минута

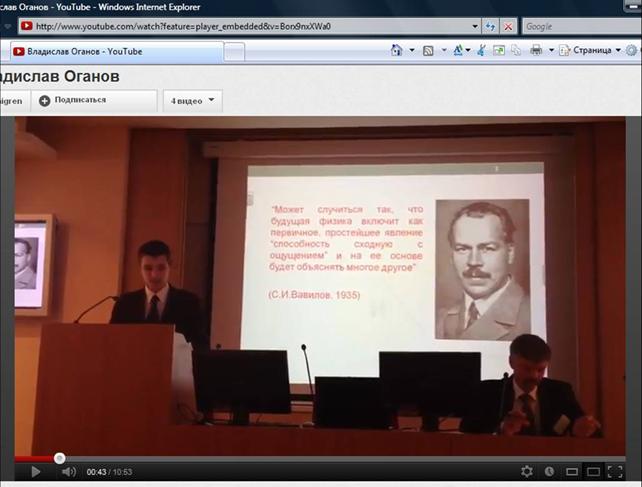
В 1935 году академик Вавилов, в проекте статьи «Физика» для Большой Советской энциклопедии, сделал следующее предположение: «Может случиться так, что будущая физика включит как первичное, простейшее явление «способность сходную с ощущением» и на ее основе будет объяснять многое другое».
 

Стр. 30, левая колонка, 1 абзац

 В 1935 году академик С.И. Вавилов, в проекте статьи “Физика” для Большой Советской энциклопедии, сделал следующее предположение: “Может случиться так, что будущая физика включит как первичное, простейшее явление “способность сходную с ощущением” и на ее основе будет объяснять многое другое” [1].
 

2 минута

 Одной из возможных верификаций прогностического высказывания академика Вавилова является синергетическая теория информации.

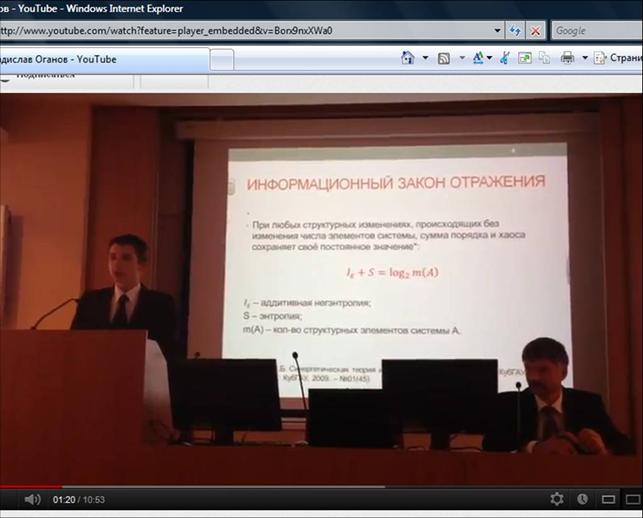
  Основой для синергетической теории информации является информационный закон отражения, согласно которому информация, отражаемая системой через совокупность своих частей, делится на отраженную и неотраженную, первая из которых представляет собой аддитивную негэнтропию и является показателем порядка, а вторая является показателем хаоса и называется энтропией отражения.

Также при любых структурных изменениях системы, происходящих без изменения числа элементов, сумма порядка и хаоса сохраняет свое постоянное значение:

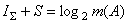
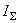 - аддитивная негэнтропия;
S – энтропия;
m(A) – кол-во структурных элементов системы А.
 

Стр. 30, левая колонка, 2 абзац

В настоящее время одной из возможных верификаций прогностического высказывания академика С.И. Вавилова может служить синергетическая теория информации (СТИ) [2].

 Ключевое положение в СТИ занимает информационный закон отражения, согласно которому информация, отражаемая системой через совокупность своих частей, разделяется на отраженную и неотраженную части, первая из которых представляет собой аддитивную негэнтропию отражения 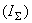 и характеризует структуру системы со стороны ее упорядоченности, а вторая, именуемая как энтропия отражения (S), является показателем структурного хаоса.

Стр. 30, правая колонка, 1-2 абзац

Но, при этом в любой системе A с фиксированным числом элементов m(A) всегда наблюдается равенство:

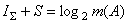
Иначе говоря, при любых структурных преобразованиях системы, происходящих без изменения числа ее элементов, сумма порядка и хаоса сохраняет свое постоянное значение.
 

3 минута

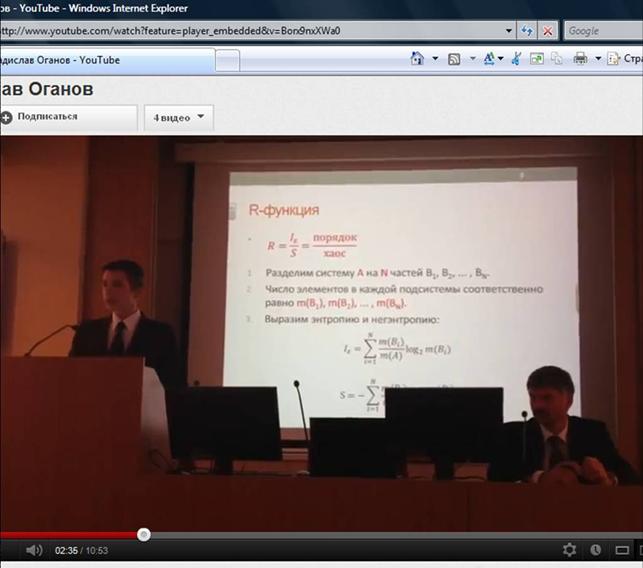
 В качестве обобщенной характеристики можно использовать так называемую R-функцию, представляющую собой отношение порядка к хаосу:

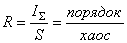
Для того, чтобы иметь более строгое представление о вышесказанном выведем формулу негэнтропии и энтропии, то есть порядка к хаосу. Соответственно

 1. Разделим систему А на N частей

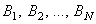
 2. Число элементов в каждой подсистемы соответственно равно .

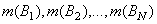 3. Выразим энтропию и негэнтропию:

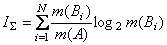
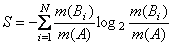
Стр. 31, левая колонка, 2-4 абзац

 Отмеченные информационные особенности отражения системных образований позволяют в качестве обобщенной характеристики их структурной организации использовать так называемую R-функцию [3], представляющую собой отношение порядка к хаосу, то есть:

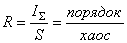
 Чтобы иметь более строгое представление о сказанном покажем чему равны в математическом отношении аддитивная негэнтропия и энтропия отражения, для чего возьмем произвольную систему А с числом элементов 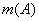 и разделим ее по какому-либо признаку на N частей 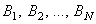 с числом элементов в каждой части соответственно равным 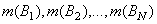. В этих обозначениях формулы аддитивной негэнтропии и энтропии отражения имеют вид:

.

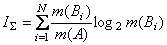
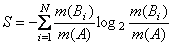
4 минута

 Возвращаясь к прогностическому высказыванию академика Вавилова начнем, так сказать, «объяснять многое другое», для чего возьмем в качестве «испытательного полигона» периодический закон Менделеева и будем исследовать элементы с точки зрения делимости атомов на электронные подоболочки.

 Для примера я взял атомы фтора и неона.

F₉:
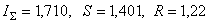
 Ne₁₀:
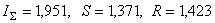
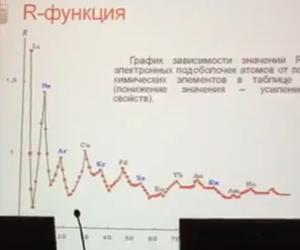
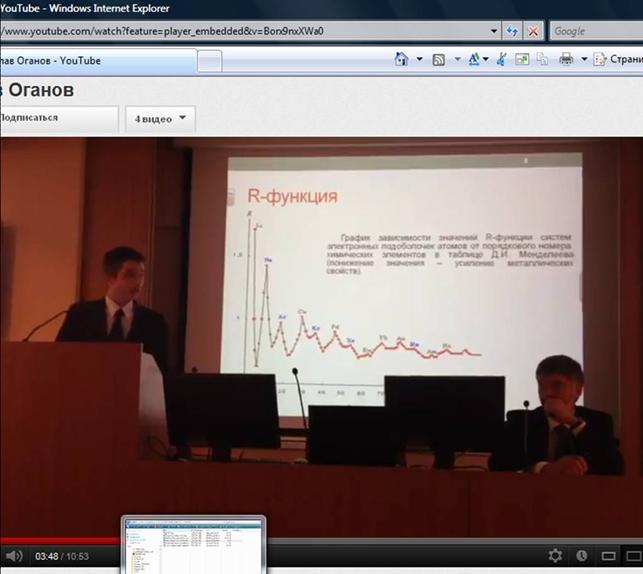
 Таким же образом были посчитаны аддитивная негэнтропия и энтропия других элементов, на основе чего был составлен данный график зависимости R-функции от порядкового номера:

Стр. 31, левая колонка, 5 абзац – правая колонка 2 абзац

 Возвращаясь теперь к прогнозу академика С.И. Вавилова, попробуем с помощью R-функции начать "объяснять многое другое", для чего возьмем в качестве "испытательного полигона" периодическую таблицу Д.И. Менделеева и будем рассматривать электронные системы атомов химических элементов со стороны их деления на электронные подоболочки.

 Например, если рассмотреть электронную систему атома неона (Ne₁₀) <…> , то <…>. Соответственно, аддитивная негэнтропия и энтропия отражения, а также R-функция равны:

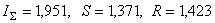
На рис. 1-3 показаны соответствующие графики R-функции в горизонтальном и вертикальном направлениях таблицы.

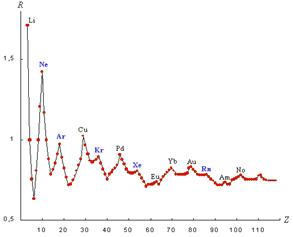
Рис. 1. График зависимости значений R-функции систем электронных подоболочек атомов от порядового номера химических элементов в таблице Д.И. Менделеева
 

5 минута

ВЫВОДЫ:

 - Также из примера следует, что чем большее разнообразие проявляют элементы системы по какому-либо признаку, тем выше энтропия отражения и ниже аддитивная негэнтропия. И, наоборот, чем более однородны элементы, тем больше аддитивная негэнтропия и меньше энтропия отражения.

- Периодичность изменения свойств химических элементов является отражением периодического изменения значений R-функции систем электронных подоболочек атомов.
 

Стр. 30, правая колонка, 1 абзац

Чем большее разнообразие проявляют элементы системы по какому-либо признаку, тем выше энтропия отражения и ниже аддитивная негэнтропия. И, наоборот, чем более однородны элементы, тем больше аддитивная негэнтропия и меньше энтропия отражения.

 Стр. 32, правая колонка, 2 абзац –
стр. 33, левая колонка, 1 абзац

 Обобщая проведенный краткий анализ структурной организации электронных систем атомов химических элементов, периодическому закону Д.И. Менделеева можно дать следующую интерпретацию: периодичность изменения свойств химических элементов является отражением периодического изменения значений R-функции систем электронных подоболочек атомов.
 

 
Комментарии

 1). В приведенных выдержках из доклада Оганова В.В. единственной самостоятельно выполненной работой докладчика является расчет значений 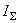, S, R для атома фтора: 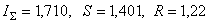. Но даже тут в расчетах допущены ошибки, поскольку действительные значения этих функций для атома фтора равны:

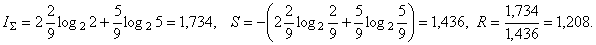
 И это при том, что такой же по своей подробности пример расчета 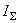, S, R приведен в статье для атома неона. То есть, докладчик, имея подробный пример расчета значений информационных функций для атома одного химического элемента, не может правильно выполнить такие же вычисления даже для атома соседнего элемента.
О каких расчетах значений 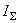 , S, R, якобы выполненных докладчиком для всех атомов химических элементов таблицы Д.И. Менделеева, можно после этого говорить?

  2). Последний вывод, сделанный в докладе, заканчивается словами: «Если продолжить график зависимости R-функции от порядкового номера, то вскоре R-функция будет равна единице»  (6-я минута доклада).
Чтобы  увидеть явное заблуждение в этих словах, достаточно посмотреть на оригинал данного графика
http://vbvvbv.narod.ru/Mendeleev_STI/index.htm . Из графика видно, что элементы со значением 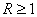 встречаются только в первой четверти периодической таблицы Д.И. Менделеева. После этого, при общем последовательном понижении значений в локальных максимумах, у всех элементов 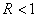. То есть, периодическое увеличение  значений R-функции имеет затухающий характер, а утверждение докладчика этому противоречит.