СИСТЕМНЫЕ ОБРАЗОВАНИЯ: ИНФОРМАЦИЯ И ОТРАЖЕНИЕ

Вяткин В.Б.

МАТЕМАТИЧЕСКИЕ МОДЕЛИ
ИНФОРМАЦИОННОЙ ОЦЕНКИ ПРИЗНАКОВ РУДНЫХ ОБЪЕКТОВ

Автореферат
диссертации на соискание ученой степени
кандидата технических наук

Екатеринбург: УГТУ-УПИ, 2004.
______________________________________________________________________________

Глава 3
(Синергетический подход к количественному определению информации)

В третьей главе разрабатывается новый подход к определению количества информации, отличительной чертой которого от традиционных подходов является отношение к информации как к снимаемой неопределенности отражения системных объектов. Этот подход получил название синергетический, что обусловлено тем, что элементы системных объектов участвуют в их отражении всей своей совокупностью, а термин синергетика в переводе с греческого языка буквально означает совместный, согласованно действующий.

В синергетическом подходе выводу формулы негэнтропии отражения предшествует определение количества информации, которую произвольный системный объект отражает о самом себе как едином целом и называемую также самоотражаемой информацией. При этом используется следующий аксиоматический базис (на примере системного объекта А).

1). Под термином информация понимаются сведения о системном объекте, как едином целом.

2). Количество информации , самоотражаемой системным объектом А, является монотонно возрастающей функцией от и, соответственно, для любых двух системных объектов А и В, таких, что , имеет место неравенство:

............................................................................(5)

3). Показателем системного объекта А, как единого целого, является интегративный код его элементов, представляющий собой индивидуальную для каждого элемента последовательность символов какого-либо алфавита, число которых (длина кода) является функцией от общего количества элементов системного объекта.

Вывод формулы проводится на основе моделирования процесса увеличения числа элементов системного объекта А в виде роста ориентированного дерева (рис. 5), совокупность висячих вершин которого взаимно-однозначно соответствует множеству элементов , а максимальное число дуг, выходящих из одной вершины, равно числу символов (n) алфавита, выбранного для составления интегративных кодов. При этом каждой из смежных дуг, в алфавитном порядке, ставится в соответствие свой символ и, как следствие, в качестве индивидуального интегративного кода какого-либо элемента выступает последовательность символов, находящихся на пути движения из начальной вершины дерева в соответствующую данному элементу висячую вершину.

Рис. 5. Модель дерева интегративных кодов при n = 2, m(A) = 6

Из анализа рис. 5 следует, что в общем случае все элементы по длине их интегративного кода (числу символов) делятся на два подмножества и , таких, что , , где - целочисленная часть . Соответственно, средняя длина интегративного кода элементов равна:

Установлено, что , в зависимости от величины n, принимает следующие значения:

, ............................................................(6)

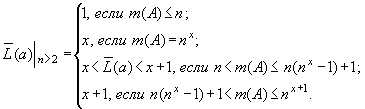......................................(7)

Из совместного анализа выражений (6) и (7) следует, что множества значений и взаимно-однозначно соответствуют друг другу только тогда, когда n = 2. Иначе говоря, только выражение (6) удовлетворяет аксиоме (5) и в силу этого оно может служить мерой количества информации , то есть:

Выявлено, что разность на всем множестве значений ограничена постоянной величиной y :

Так как , а является монотонно возрастающей функцией от , значения которой удовлетворяют информационной аксиоме (5), то, учитывая значение постоянной y , в практическом отношении (в том числе для простоты расчетов) принимается эквивалентность:

Интегративный код любого элемента представляет собой определенное символьное сообщение о системном объекте А, как о целостном образовании, вследствие чего величина информации интерпретируется также, как средняя длина такого сообщения. Исходя из этого, формула негэнтропии отражения выводится на основе анализа процесса передачи информации по системе информационной связи, в которой отражаемый (A) и отражающий (B) системные объекты являются, соответственно, источником и приемником информации, а связующий объект выступает в качестве передающей среды или канала связи. При этом адресатом является познающий субъект. В результате указанного анализа формула негэнтропии отражения системных объектов получена в следующем виде:

........................................................... (8)

Из выражения (8) следует, что негэнтропия является частью средней длины интегративного кода элементов . Так как связующий объект K является подмножеством как системного объекта А, так и системного объекта В, то утверждается, что величина негэнтропии представляет собой общую часть средней длины интегративного кода элементов и .

Главная страница