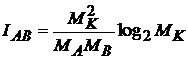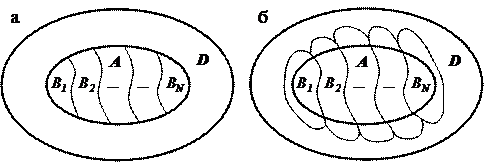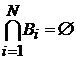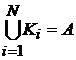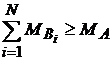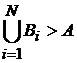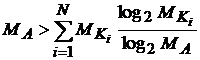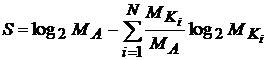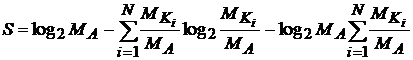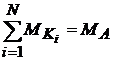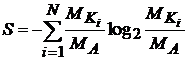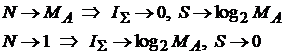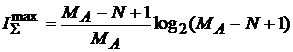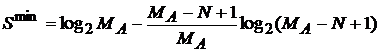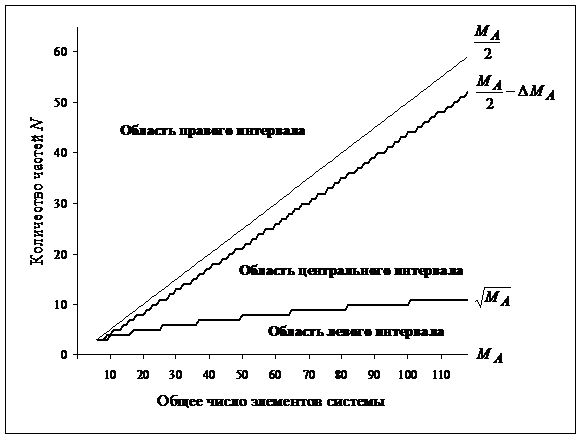СИСТЕМНЫЕ ОБРАЗОВАНИЯ: ИНФОРМАЦИЯ И ОТРАЖЕНИЕ

Вяткин В.Б.

Синергетическая теория информации

Часть 2. Отражение дискретных систем в плоскости признаков их описания

В статье проведён анализ отражения дискретной системы с конечным множеством элементов в плоскости множества значений произвольного признака. Доказано, что отражаемая системой информация делится на отражённую и неотражённую части и получены соответствующие информационные функции. Установлен структурный закон сохранения суммы хаоса и порядка и дана классификация дискретных систем по их структурной организации. Показана взаимосвязь синергетической и вероятностной теорий информации. Установлен закон сохранения информации.

«Не видно, почему теория информации должна столь
 существенно основываться на теории вероятностей,
как это представляется по большинству руководств»

Колмогоров А.Н.

Введение

В предыдущей статье автора [1], опубликованной в настоящем издании, был изложен новый – синергетический – подход к определению количества информации и получена формула негэнтропии отражения , то есть количества информации, которую отражают (воспроизводят) друг о друге, как о целостном образовании, два пересекающихся конечных множества А и В, таких, что , . При количестве элементов в составе каждого из множеств  равном, соответственно, , формула негэнтропии отражения имеет вид:

.                                                        (1)

При этом напомним, что гносеологически формула (1) относится к ситуации, когда множества А и В выделены в составе некоторой дискретной системы  при её рассмотрении в соответствующих плоскостях единичных значений признаков  и .

Развивая в настоящей статье синергетический подход к определению количества информации, будем считать, что множество  представляет собой автономную систему (подсистему ), и начнём рассмотрение информационных аспектов её отражения через совокупность конечных множеств , выделенных в составе системы D по множеству значений признака  (также может рассматриваться в качестве отражающей автономной системы). При этом предварительно сделаем следующие замечания.

1). Будем анализировать только те ситуации, когда отражающие множества ,  не пересекаются друг с другом и каждый элемент отражаемой системы А характеризуется конкретным значением признака (рисунок 1).

а – система А информационно закрыта;   б – система А информационно открыта

Рисунок 1. Отражение системы  через совокупность

конечных множеств

То есть:

,   

 и, соответственно:

,  

2). Отражаемая система А по отношению к окружающей среде (элементам дополняющего множества ) может быть как открытой, так и закрытой в информационном отношении.

Система А в плоскости признака  является закрытой в информационном отношении, если отсутствует её непосредственная взаимосвязь с окружающей средой (рисунок 1а), то есть:

,   .

Система А в плоскости признака  является открытой в информационном отношении, если наблюдается её непосредственная взаимосвязь с окружающей средой (рисунок 1б), то есть:

,  

3). Количество любой информации, измеряемой с помощью двоичных логарифмов, традиционно принято выражать в битах (слово бит, как сокращённое название двоичной единицы (binary digit), было предложено Тьюки [2]). То есть . Так как в развиваемой нами теории, при оценке отражаемой информации, могут использоваться только двоичные логарифмы [1], то мы не будем отходить от этой традиции. Вместе с тем, если в традиционной теории информации 1бит интерпретируется как максимальное количество информации, которое можно получить при выборе одной из двух возможностей, то в синергетической теории информации за 1бит принимается количество информации, самоотражаемой двоичным множеством или системой, состоящей из двух элементов. Чтобы отличать друг от друга эти численно равные единицы измерения различных видов информации (связанной с управлением и существующей независимо от него), будем называть их бит управления и бит отражения, соответственно.

С учётом сделанных замечаний перейдём к непосредственному рассмотрению особенностей отражения системы А через совокупность конечных множеств (систем)  и начнём со случая, когда отражаемая система является закрытой в информационном отношении.

Отражение информационно закрытых систем

Количество информации , отражаемое системой А, о самой себе, как о целостном образовании, согласно работе [1] равно:

                                                                         (2)

По значениям признака  система делится на N частей в виде совокупности конечных множеств , каждое из которых отражает о системе определённую информацию, численно равную негэнтропии отражения (1). Соответственно, общее количество информации о системе А, отражаемое через совокупность её частей, равно аддитивной негэнтропии отражения , формула которой в условиях информационной закрытости системы  имеет вид:

                                                 (3)

При анализе отражения системы А через совокупность своих частей, информация  и аддитивная негэнтропия  выступают перед нами в качестве отражаемой и отражённой информации, соответственно. Проведём их сравнение, для чего правые части выражений (2) и (3) умножим на  и разделим на . В результате этой операции для  получаем очевидное неравенство

,

из которого следует, что

Иначе говоря, не вся информация о системе А, как едином целом, отражается через совокупность её частей и всегда существует некоторая часть информации , которая остаётся неотражённой.

Является очевидным, что аддитивная негэнтропия отражения и неотражённая информация по отношению друг к другу выступают в качестве взаимодополняющих противоположностей и характеризуют отражение дискретных систем через свои части с различных сторон, – определённости и неопределённости, соответственно. Это позволяет говорить о том, что неотражённая информация представляет собой энтропию отражения. Обозначим энтропию отражения символом S и определим её величину как разность между отражаемой и отражённой информациями:

                                                                           (4)

В соответствии с формулами (2) и (3) запишем:

                                                     (5)

Умножив и разделив аргумент второго логарифма в выражении (5) на , и заменяя при этом логарифм произведения суммой логарифмов, получаем:

Так как , то из последнего выражения следует:

                                                               (6)

Из выражений (3) и (6) видно, что  при постоянстве  величина аддитивной негэнтропии  и энтропии отражения S зависит от количества частей системы и их соотношения между собой по числу элементов. При этом, чем более раздробленной является структура системы или, что то же самое, чем более разнообразны и неупорядочены её элементы по значениям признака, в плоскости которого идёт рассмотрение системы, тем больше энтропия S и меньше аддитивная негэнтропия . И, наоборот, – чем меньше частей выделяется в составе системы и, соответственно, чем более однообразны и упорядочены её элементы по значениям признака, тем больше  и меньше S. Так как  и S не могут превышать отражаемую информацию , а число частей системы N не может быть больше общего количества её элементов , то сказанное формализуется следующим образом:

                                                   (7)

Иначе говоря, увеличение числа отражающих конечных множеств приводит к возрастанию хаотичности, неупорядоченности, неопределённости отражения дискретной системы, как единого целого. То есть, чем более неадекватно отражение, тем больше его энтропия и меньше аддитивная негэнтропия.

Так как структуру любой системы, в первую очередь, характеризуют количество её частей и взаимоотношение последних по числу элементов, то также можно утверждать, что аддитивная негэнтропия и энтропия отражения, по отношению к структуре отражаемой системы, выступают в качестве показателей её упорядоченности и хаотичности или, выражаясь другими словами, являются мерами структурного хаоса и порядка, соответственно. Проиллюстрируем это следующим примером.

На рисунке 2 приведены различные состояния системы, состоящей из 16-ти элементов, которые характеризуются признаком «направление движения». По значениям этого признака система последовательно принимает 5 состояний, которым соответствует её деление на 1, 2, 4, 8, 16 равновеликих частей.

Рисунок 2. Деление системы на равновеликие части по признаку

«направление движения элементов»

В состоянии на рисунке 2а все элементы движутся в одном направлении, и в структуре системы наблюдается идеальный порядок. На рисунке 2д имеем полярную противоположность, то есть каждый элемент системы обладает строго индивидуальным направлением движения и структура системы является максимально хаотичной. Состояния системы на рисунках 2б,в,г занимают промежуточное положение по отношению к состояниям на рисунках 2а,д и характеризуются тем, что в их структуре присутствует как хаотичность, так и упорядоченность. Рассчитывая для каждого состояния системы по формулам (3) и (6) значения аддитивной негэнтропии и энтропии отражения, получаем[1]:

Из приведённых результатов видно, что нарастанию хаоса и уменьшению порядка в структуре системы на рисунке 2 соответствует уменьшение значений аддитивной негэнтропии и увеличение значений энтропии отражения.

Аддитивная негэнтропия , как отражённая информация, и энтропия отражения S, как неотражённая информация, являются составными частями отражаемой информации , в силу чего имеет место равенство

                                                                        (8)

В то же самое время, как было показано,  и S количественно характеризуют структуру отражаемой системы со стороны её упорядоченности и хаотичности. Поэтому равенство (8) также показывает, что при фиксированном числе элементов системы сумма хаоса и порядка в её структуре остаётся постоянной величиной. Иначе говоря, чтобы мы ни делали с системой без изменения общего количества элементов, на сколько бы частей не разбивали её по значениям какого-либо признака и в каком бы соотношении по числу элементов не находились между собой части, сумма хаоса и порядка в структуре системы всегда будет оставаться неизменной. То есть, можно констатировать, что при любых структурных преобразованиях системы, происходящих без изменения числа её элементов, имеет место закон сохранения суммы хаоса и порядка:

порядок + хаос = const

Например, для вышеописанной системы на рисунке 2, как это видно из результатов проведённых расчётов, по всем её состояниям имеем: .

Хаотичность и упорядоченность в своей совокупности определяют в целом структурную организацию системы и, соответственно, для ее количественной характеристики может использоваться та или иная функция, аргументами которой являются меры хаоса и порядка. В качестве такой функции структурной организации может использоваться так называемая R-функция[2], представляющая собой отношение аддитивной негэнтропии к энтропии отражения:

                                                                   (9)

То есть значения R-функции говорят о том, что и в какой мере преобладает в структуре системы: хаос или порядок. Так, если R > 1, то в структуре системы преобладает порядок, в противном случае, когда R < 1 – хаос. При R = 1 хаос и порядок уравновешивают друг друга, и структурная организация системы является равновесной. Например, для различных структурных состояний системы на рисунке 2 значения R-функции равны:

 Рассмотрим теперь особенности взаимоотношений аддитивной негэнтропии  и энтропии отражения S при постоянном числе элементов системы  и различном количестве частей N, соотносящихся между собой по числу элементов  произвольным образом. При этом, сначала определим максимальные и минимальные значения  и S при данном N, основываясь на формулах (3) и (6) и выражениях (7) и (8).

Энтропия отражения является максимальной, когда все части системы представлены одинаковым числом элементов, то есть:

                                                       (10)

Соответственно, минимальная величина аддитивной негэнтропии отражения имеет вид:

                                                 (11)

Максимальное значение, в свою очередь, аддитивная нгэнтропия будет принимать тогда, когда число элементов в одной части равно , а каждая из остальных  частей включает в себя только 1 элемент, то есть:

                                                            (12)

Соответственно, минимальная величина энтропии отражения равна:

                                               (13)

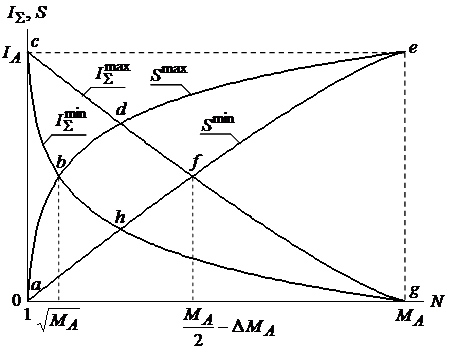
Построим графики , как функций от N и проведём анализ полученной диаграммы, которую будем называть информационным полем отражения дискретных систем (рисунок 3).

Рисунок 3. Информационное поле отражения дискретных систем

( M_A = 118 )

Приведённые графики изначально образуют два контура: энтропийный – abdefha и негэнтропийный или информационный – cdfghbc, которые локализуют соответствующие области всех возможных значений энтропии и аддитивной негэнтропии отражения информационно закрытых систем. Пересечение этих контуров по точкам b и f, где наблюдаются равенства  и , позволяет по их проекциям выделить на горизонтальной оси три интервала значений N (левый, центральный, правый) с присущими каждому интервалу особенностями взаимоотношений  и S. Рассмотрим эти особенности, предварительно определив значения N, соответствующие точкам b и  f.

В точке b, согласно правым частям выражений (10) и (11), имеем уравнение , решение которого даёт, что в соответствующей проекции .

При этом необходимо отметить, что поскольку N может принимать только целочисленные значения, то границы интервалов определяются с точностью до ближнего большего целого. Аналогичное уравнение для точки f, образованное правыми частями выражений (12) и (13) не имеет аналитического решения. То есть, значение N, соответствующее проекции точки f, точно может быть определено только численным путём.  (Для членов последовательности N = 1, 2, …,  определяются  и , и в качестве значения N, соответствующего точке f, принимается то значение, после которого .) Но при этом, как показывают расчёты, значение N остаётся меньше  на некоторую величину , которая увеличивается по мере роста  (рисунок 4). То есть, точке f  на оси N соответствует значение .

Таким образом, при заданном  имеем три формализованных интервала значений N:

- левый:  ;

- центральный:  ;

- правый:  .

Форма границ интервалов и соответствующие области возможных значений N, в зависимости от величины , иллюстрируются рисунком 4. При этом графики начинаются с , так как при  центральный интервал, как таковой, просто не существует.

Рисунок 4. Области интервалов значений N

Отражение систем, попадающих в левый интервал (см. рисунок 3), характеризуется тем, что при любых соотношениях их частей между собой по числу элементов, сохраняется неравенство . То есть, в левом интервале значений N структурная упорядоченность системы всегда больше её хаотичности и .

В правом интервале наблюдается противоположная картина, когда при любых структурных преобразованиях системы выполняется неравенство , что соответствует погашению отражаемой информации и преобладанию хаоса над порядком. При этом .

В центральном интервале происходит пересечение областей возможных значений  и S, вследствие чего между ними здесь наблюдаются различные соотношения и проявляется тенденция к взаимному уравновешиванию структурного порядка и хаоса. R-функция при этом может быть как больше, так и меньше единицы, а в ряде случаев (по линии bf ) имеет место и равенство .

Иначе говоря, в левом интервале значений N наблюдается необратимое преобладание в структуре системы порядка над хаосом, а в правом интервале, наоборот, – необратимое преобладание хаоса над порядком. В центральном интервале, в свою очередь, преобладание как порядка над хаосом, так и хаоса над порядком является обратимым. Чтобы отчётливо представлять, что значит порядок левого интервала и хаос правого, а также гармония их взаимоотношений в центральном интервале, приведём образные лингвистические примеры.

Любой текст, как дискретная система с конечным множеством элементов, может быть рассмотрен в плоскости алфавита, с помощью которого он написан. Совокупности одинаковых букв при этом образуют отдельные части системы и, соответственно, для анализа структуры текста может использоваться материал настоящего раздела. Проведём такой анализ текстов, полученных различными исполнителями.

Возьмём известную обезьяну-машинистку, с которой «работал» французский математик Э.Борель, ожидая, что когда-нибудь получит от неё шекспировские строки. Проводя мысленный эксперимент, посадим обезьяну за пишущую машинку (клавиатуру компьютера). Обезьяна, случайным образом ударяя по клавишам, получает чехарду букв, лишённую всякого смысла. Такой текст олицетворяет хаос правого интервала, а его R-функция равна нулю (при длине текста, не превышающем количество букв алфавита). Посадим теперь за другую пишущую машинку дятла, который начинает методично бить по одной и той же клавише, и выдаёт однобуквенную последовательность. Текст дятла также лишён какого-либо смысла и находится в крайней левой части левого интервала, где идеальный порядок. R-функция при этом устремляется в бесконечность.

Сам собой напрашивается вывод, что наполненные смыслом содержательные тексты, по своей структурной организации, должны находиться в центральном интервале, а их R-функция должна стремиться к единице. Чтобы проверить это, пригласим А.С. Пушкина и, посадив его за третью пишущую машинку, попросим что-нибудь напечатать. Явившийся нам при этом текст, представляет собой четырнадцатистишия поэмы «Евгений Онегин», каждое из которых находится в центральном интервале, а значения R-функции равны:1-е четырнадцатистишие – R = 0.94; 2-е – R = 0.95; 3-е – R = 0.95  и т.д. То есть, А.С. Пушкин подтвердил наши предположения, показав, что содержательные, наполненные красотой и гармонией тексты, находятся в центральном интервале, а хаос и порядок в их структуре уравновешивают друг друга.

В собственно лингвистическом отношении сказанное, по-видимому, означает, что принадлежность текстов к центральному интервалу (при их длине до , где N – число символов алфавита) является необходимым условием для наличия в них содержательного смысла. Но это необходимое условие не является достаточным, так как, например, обезьяний текст, при достаточно долгом его печатании, выйдет из правого интервала и войдёт в центральный, откуда в дальнейшем перейдёт в левый, где останется навсегда. При этом, при движении текста по центральному интервалу, мы навряд ли увидим в нём хотя бы одну строку из «Евгения Онегина».

Указанные особенности интервалов значений N позволяют любые дискретные системы с конечным множеством элементов, в зависимости от количества частей, на которые они разделяются в плоскости какого-либо признака, формализовано классифицировать на три типа:

- упорядоченные (левый интервал);

- синергетичные (центральный интервал);

- хаотичные (правый интервал).

Например, система на рисунке 2 в различных своих состояниях будет представляться как: а – упорядоченная; б – упорядоченная; в – синергетичная; г – хаотичная; д – хаотичная. Точно также в приведённых лингвистических примерах олицетворением различных типов систем являются: текст дятла – упорядоченная система; текст обезьяны – хаотичная система; четырнадцатистишия «Евгения Онегина» – синергетичная система.

Заканчивая характеристику отражения информационно закрытых систем, отметим, что информационно-синергетические функции хаоса и порядка  и приведенная классификация систем имеют универсальный характер и могут использоваться при структурном анализе системных образований в любой предметной области.

Отражение информационно открытых систем

При информационном открытии системы (см. рисунок 1б) осуществляется её непосредственная взаимосвязь (взаимодействие) с окружающей средой, в результате чего часть отражаемой информации  переходит в окружающую среду и распределяется по элементам дополняющих множеств . Соответственно, по отношению к информационно закрытому состоянию системы, уменьшается аддитивная негэнтропия и увеличивается энтропия отражения. То есть собственно отражение системы становится более неопределённым, рассеянным, хаотичным. Так как отношение  не зависит от того, открыта или закрыта

система, то энтропия S (6), являясь функцией внутреннего строения системы, при информационном открытии последней не изменяется, то есть является инвариантной величиной относительно любых взаимоотношений системы с окружающей средой. Это говорит о том, что при открытии системы, в общей энтропии её отражения, появляется новая составляющая , как функция, характеризующая взаимосвязь системы с внешней средой. В соответствии со сказанным, для того, чтобы отличать друг от друга энтропии S и , будем пользоваться терминами внутренняя (S) и внешняя  энтропия отражения.

Определим величину внешней энтропии отражения, исходя из соблюдения баланса между отражаемой информацией, с одной стороны, и отражённой (негэнтропия) и неотражённой (энтропия) информациями, с другой стороны. Так как отражаемая информация  и внутренняя энтропия S при информационном открытии системы не изменяются, то внешняя энтропия  равна соответствующему уменьшению аддитивной негэнтропии отражения  информационно закрытого состояния системы:

 ,                                                                      (14)

где  – аддитивная негэнтропия отражения информационно открытой

системы.

Освободимся в выражении (14) от аддитивной негэнтропии , как структурной характеристики закрытых в информационном отношении систем, для чего перепишем его в развёрнутом виде и проведём несложные преобразования.

Умножив и разделив полученное выражение на , имеем:

                                               (15)

Первый сомножитель в выражении (15) представляет собой отношение количества элементов дополняющего множества  к числу элементов связующего множества .  Иначе говоря  этот сомножитель есть отношение области непосредственной взаимосвязи множества  с окружающей систему A средой к области непосредственной взаимосвязи этого же множества с самой системой A. Так как гносеологически множество  относится к результатам рассмотрения системы А в плоскости признака , то данный сомножитель будем называть коэффициентом  информационной открытости системы по i-му значению признака , то есть:

,                                                          (16)

Совокупность второго и третьего сомножителей, в свою очередь, представляет собой негэнтропию отражения  открытой системы. Поэтому, с учётом (16), формула внешней энтропии  имеет вид:

                                                                    (17)

Вернёмся теперь к рассмотрению информационного поля отражения дискретных систем на рисунке 3. Является очевидным, что прямоугольный контур aceg ограничивает в целом площадь информационного поля, включающего в себя, при данном , все возможные значения аддитивной негэнтропии и энтропии отражения, как открытых, так и закрытых в информационном отношении систем. В предыдущем разделе было показано, что если система является информационно закрытой, то области возможных значений аддитивной негэнтропии и энтропии отражения ограничены контурами cdfghbc и abdefha, соответственно. Когда система информационно открывается, её отражение становится более неопределённым и области возможных значений, как аддитивной негэнтропии, так и энтропии отражения начинают увеличиваться. При этом новые возможные значения аддитивной негэнтропии располагаются ниже линии , а энтропии отражения, – выше линии . В случае неограниченного возрастания общего информационного открытия системы, то есть когда

,

минимум аддитивной негэнтропии и максимум общей энтропии отражения выходят на свои асимптотические значения, лежащие, соответственно, на линиях ag и ce. При этом полностью задействуются три новых области информационного поля отражения: abca, ahga и cdec. Причём, в первую из указанных областей попадают значения, как аддитивной негэнтропии, так и энтропии отражения, а вторую и третью области занимают, соответственно, только значения одной из них. Таким образом, комплексные области возможных значений отражённой и неотражённой информации ограничены контурами: аддитивная негэнтропия отражения – acdfga, энтропия отражения – acefga. Заканчивая описание распределения отражаемой информации по информационному полю отражения acega, отметим также, что в его пределах существует довольно обширная область efge, в которую никогда не попадают значения как отражённой, так и неотражённой информации.

Информационный закон отражения

На основе изложенного материала составим информационный баланс отражения дискретных систем для общего случая, соответствующего состоянию информационной открытости системы:

                                                                 (18)

Если система информационно закрывается, то есть перестаёт взаимодействовать с окружающей средой, то  и информационный баланс отражения принимает форму выражения (8).

Полученное выражение (18) является устойчивым, однозначным соотношением между отражаемой, отражённой и неотражённой информациями, справедливым для любых дискретных систем, представленных конечным множеством элементов, вне зависимости от степени их информационной открытости, количества отражающих объектов и их соотношения между собой по числу элементов, что позволяет придать ему статус закона. Дадим этому закону название информационный закон отражения и сформулируем его следующим образом: при отражении системы А через совокупность систем , таких, что ,  и , происходит разделение отражаемой информации на отражённую и

неотражённую части, первая из которых равна аддитивной негэнтропии, а вторая – сумме внутренней и внешней энтропий отражения.

Установленный закон по своей форме подобен известным физическим законам, таким как закон сохранения энергии, закон сохранения количества движения и т.д. При этом особо отметим, что на необходимость установления подобного рода законов в теории информации указывалось математиками и философами ещё в 50-е – 60-е годы прошлого столетия. Так, например, академик А.А. Харкевич писал: «Несмотря на быстрые темпы развития, общая теория связи (теория информации – прим. В.В.) не получила еще завершения в своих основных построениях. Обращает на себя внимание, в частности, отсутствие до настоящего времени системы основных законов типа законов сохранения, характерных для многих сложившихся отраслей знания. Наличие подобного рода законов, специфичных для связи, интуитивно ощущается. Однако эти законы еще не найдены и не сформулированы» [3, с.89]. Еще более близки к установленному нами закону философские заключения И.Б. Новика [4], который первым предложил трактовать информацию как форму отражения и считать, что информация – это упорядоченность отражения, а шум – неупорядоченность, хаотичность отражения. При этом было сделано предположение, фактически точно предсказывающее выражение (8): «Закон сохранения отражения в замкнутой системе может быть представлен в виде: I+N=const, где I –   количество информации, а N (от англ. слова noise – шум) – количество шума, то есть суммарное количество отражения в замкнутой системе – величина постоянная» [4, с.127]. Это философское предсказание до получения выражений (8) и (18) не имело аналитического подтверждения, так как существующая теория информации не могла предоставить для измерения информации и шума (энтропии) различные функции, сумма значений которых оставалась бы постоянной. В связи с этим, проводя параллели с физическими законами сохранения, тот же И.Б. Новик говорил: «Если рассматривать одну какую-нибудь форму энергии (например, тепловую), то сохранения этой формы мы не обнаружим. Подобно этому, по-видимому, и при рассмотрении только одной формы отражения (информации) без учёта её перехода в другую форму закон сохранения в данной области не удаётся установить» [4, с.127].

Изложенный материал свидетельствует, что нами получены три информационные формы отражения  и показаны их взаимные переходы друг в друга при сохранении суммарного количества информации. Вместе с тем, мы воздерживаемся в настоящем разделе интерпретировать выражения (8) и (18) как закон сохранения информации (хотя их трактовка, как закона сохранения отражения, вполне допустима). Причина этого заключается в следующем. – Как было показано ранее [1], в синергетической теории информации мы имеем дело с тем видом информации, который существует независимо от управления, и созвучно названию теории может именоваться как синергетический вид информации. Другой же вид информации, неразрывно связанный с управлением и называемый вероятностным видом, при этом специально не рассматривается. Изучением этого вида информации занимается традиционная или вероятностная теория информации, основанная на рассмотрении множества вероятностей ансамбля случайных величин. То есть, дихотомически существуют два вида информации, каждому из которых соответствует своя теория со своим математическим аппаратом. Поэтому, прежде чем говорить о законе сохранения информации в более широком смысле, чем просто закон сохранения отражения, необходимо рассмотреть взаимоотношения синергетической и вероятностной теорий информации.

Сравнительная характеристика

синергетической и вероятностной теорий информации

Отношение  в выражении (6) с позиций теории вероятностей представляет собой вероятность  встречи элементов, обладающих i-м значением признака , среди общего числа элементов системы А. Поэтому формула энтропии отражения информационно закрытых систем (6) может быть представлена также в следующем виде:

                                                                      (19)

Полученная формула (19) широко известна в науке как энтропия множества вероятностей Шеннона [2] и занимает в традиционной теории информации фундаментальное положение, являясь мерой количества информации, возможности выбора и неопределённости.[3] Данный факт говорит о том, что вероятностная и синергетическая теории информации, имея предметом своего познания различные виды информации (связанной с управлением и существующей независимо от него), в то же самое время непосредственно взаимосвязаны между собой отношением взаимного проникновения друг в друга и, как следствие, в своей совокупности образуют единую количественную теорию информации. Образно выражаясь, можно сказать, что синергетическая и вероятностная теории информации являются оборотными сторонами одной и той же медали, название которой – «количество информации». В качестве переходного мостика при этом выступает энтропия (19), играющая в данных теориях различную роль.

В то же время необходимо отметить следующее. – В теории информации Шеннона энтропия (19) вводится в рассмотрение эмпирическим путём в самом начале теории, как функция, удовлетворяющая требованиям, априорно предъявленным к мере неопределённости выбора одной из N различных по своим вероятностям возможностей. В синергетической теории информации, в свою очередь,  энтропия (19) получена аналитическим путём в процессе анализа отражения информационно закрытых систем, как разность между отражаемой и отражённой информациями. Иначе говоря, в синергетической теории информации энтропия (19) представляет собой меру неотражённой информации для информационно закрытых систем, и в силу этого является вторичной, то есть выводимой через негэнтропию отражения функцией. Сказанное приводит нас к выводу, что с информационно-генетических позиций синергетическая теория информации является первичной по отношению к вероятностной теории информации Шеннона. При этом следует отметить, что данное утверждение полностью согласуется с выводом академика А.Н. Колмогорова о том, что «теория информации должна предшествовать теории вероятностей, а не опираться на неё» [5, с. 249].[4]

Продолжая сравнение теорий, и обращаясь при этом к диаграмме на рисунке 3, можно видеть, что в собственно информационном отношении вероятностная теория информации ограничена энтропийным контуром abdefha. Остальная часть информационного поля отражения дискретных систем, в отличие от синергетической теории информации, остаётся для неё недоступной. Иначе говоря, сфера приложения теории информации Шеннона ограничена информационно закрытыми системами. Но даже в этих условиях основополагающая информационно-энтропийная мера Шеннона, взятая сама по себе, является инвариантной функцией относительно размеров структурно-подобных систем.  (Структурно-подобными мы называем системы, в составе которых выделяется одинаковое количество частей и наблюдается одно и то же пропорциональное соотношение последних по числу элементов.) Примеры таких систем приведены на рисунке 5.

Рисунок 5. Структурно-подобные системы

Проводя для приведённых структурно-подобных систем , ,  соответствующие расчёты, получаем:

                                     Система:          

              Энтропия Шеннона (S):     2      2      2

             (энтропия отражения)

  Аддитивная негэнтропия :     0      2     4

                                  R-функция:     0      1     2

Как видим, энтропия Шеннона для всех трёх систем имеет одинаковое значение, то есть не отличает эти системы друг от друга. В то же время, поскольку S и  согласно (8) реагируют на структурные изменения систем равносильным образом, то приведённые расчёты также показывают, что уже только одна аддитивная негэнтропия отражения является более универсальным инструментом анализа информационно закрытых систем по сравнению с информационно-энтропийной мерой Шеннона. Более же полное использование аппарата синергетической теории информации позволяет формализовано классифицировать каждую из систем ,, на рисунке 5, как хаотичную, синергетичную и упорядоченную, соответственно (чего, естественно, теория Шеннона сделать не может).

Обобщая сказанное, и подчёркивая, что в традиционной теории информации фигурирует только одна из трёх информационно-синергетических функций , логично утверждать, что общий потенциал практического использования у синергетической теории информации должен быть больше, чем у вероятностной теории информации Шеннона. Реализация этого потенциала является вопросом времени.

Закон сохранения информации

Представление внутренней энтропии отражения в виде формулы (19) свидетельствует о том, что одна из разновидностей синергетической информации тождественна вероятностному виду информации. Поэтому, рассматривая внутреннюю энтропию S как количество вероятностной информации и, проводя соответствующую интерпретацию равенств (8) и (18), можно утверждать, что эти равенства на межвидовом информационно-количественном уровне выражают закон сохранения информации, который, в зависимости от того, какими являются системы в информационном отношении, может быть сформулирован следующим образом.

Информационно закрытые системы: В информационно закрытых  системах с конечным множеством элементов суммарное количество синергетической и вероятностной информации сохраняет своё постоянное значение при любых структурных преобразованиях систем.

Информационно открытые системы: Общее суммарное количество вероятностной и синергетической информации, как находящейся внутри информационно открытых систем с конечным множеством элементов, так и передаваемой этими системами в окружающую среду, и получаемой ими из окружающей среды, сохраняет своё постоянное значение при любых структурно-системных преобразованиях и взаимоотношениях систем с окружающей средой.

Раскроем содержание установленного закона сохранения информации, для чего представим его в иллюстративной форме, как это показано на рисунке 6.

а – информационно закрытая система

б – информационно открытая система

Рисунок 6. Графическое выражение закона сохранения информации

Информационно закрытые системы. Когда система является закрытой в информационном отношении (см. рисунок 1а), в ней совместно с вероятностной информацией S присутствует только одна разновидность синергетической информации в виде аддитивной негэнтропии отражения  (рисунок 6а).

При этом изменение соотношения между различными видами информации и их взаимные переходы друг в друга определяются тем, в каком направлении осуществляются структурные преобразования системы. Так, например, если количество частей системы уменьшается, а тем более, если при этом какая-то часть системы начинает доминировать по числу элементов, то возрастает количество синергетической информации и уменьшается количество вероятностной. В пределе, когда все элементы системы в плоскости какого-либо признака становятся неотличимыми друг от друга и, соответственно, система не разделяется на части , её вероятностная информация полностью переходит в синергетическую информацию и как вид перестаёт существовать в системе. Разнообразия элементов и возможности выбора при этом нет и биты управления трансформируются в биты отражения. При обратных структурных преобразованиях, когда система всё более делится на части, то есть увеличивается разнообразие её элементов и возрастают возможности выбора, идёт противоположный информационный процесс. Синергетическая информация при этом переходит в вероятностную и биты отражения становятся битами управления. Этот процесс исчерпывает себя и прекращается, когда количество частей системы становится равным числу её элементов .

Так как суммарное количество синергетической и вероятностной информации в системе не изменяется, то каждый из отмеченных противоположных процессов в информационно-количественном отношении заканчивается одним и тем же результатом, математически выражаемым чисто комбинаторной формулой количества информации. При этом, в первом случае, когда уменьшается количество частей и в структуре системы возрастает порядок, мы приходим к формуле количества информации, самоотражаемой конечным множеством [1], а во втором случае, при максимальной хаотичности структуры, имеем двоичный логарифм Хартли [6], лежащий в основе традиционного комбинаторного подхода к определению количества информации [7]. То есть, по-видимому, можно сказать, что комбинаторное количество информации, в зависимости от того, с какой стороны его рассматривать, может относиться, как к синергетическому, так и к вероятностному виду информации и измеряться, соответственно, в битах отражения или в битах управления.

Рассматривая теперь математическую форму закона сохранения информации, в свете сказанного можно утверждать, что выражение (8), помимо прочего, представляет собой уравнение взаимосвязи различных подходов к количественному определению информации, что позволяет сделать методологический вывод. – Комбинаторный, вероятностный и синергетический подходы к определению количества информации неразрывно взаимосвязаны между собой и в своей совокупности составляют единую количественную основу общей теории информации.

Информационно открытые системы. Когда система информационно открывается (см. рисунок 1б), начинается её взаимодействие с окружающей средой, в результате чего часть синергетической информации  переходит в окружающую среду в виде внешней энтропии отражения  (рисунок 6б).

Если в последующем система начинает обратно закрываться , то эта информация возвращается в систему в виде соответствующего увеличения значений . Так как по определению , то независимо от степени увеличения открытости системы , при данной её структуре, во внешнюю среду может перейти только ограниченное количество информации. То есть: система не может отдать во внешнюю среду, а также получить обратно из внешней среды количество информации, превосходящее аддитивную негэнтропию отражения её информационно закрытого состояния.

Также как в случае информационной закрытости, рассмотрим два полярных друг другу структурных состояния системы. В первом случае, когда система предельно упорядочена , в ней актуализирована только синергетическая информация и до открытия системы имеем: , . После информационного открытия системы и его неограниченного возрастания , из системы выходит и распространяется по окружающей среде практически вся информация о ней, как едином целом и, соответственно: ,

Во втором случае, при максимальной хаотичности структуры системы , вся её информация представлена только вероятностным видом, который инвариантен относительно взаимоотношений системы с внешней средой. Соответственно, как до открытия системы, так и после её открытия сохраняются равенства  и , говорящие о том, что при любой степени открытости системы . Иначе говоря, достигая максимально возможной структурной хаотичности, система становится «невидимой»  для внешней среды или, выражаясь по-другому, множество  в плоскости признака , при  перестаёт восприниматься окружающей средой как система.

Заключение

В двух статьях, на основе простого аксиоматического базиса, без опоры на теорию вероятностей и традиционную теорию информации, пройден путь от рассмотрения элементарного конечного множества до установления на межвидовом информационно-количественном уровне закона сохранения информации и его частной формы, – структурного закона сохранения суммы хаоса и порядка. При этом получены неизвестные ранее информационно-количественные функции, и в то же время показана их непосредственная взаимосвязь с традиционными мерами информации (комбинаторной и вероятностной). Всё это говорит о том, что в лице синергетической теории информации мы имеем вполне сформировавшуюся новую научную теорию.

Дальнейшее развитие этой теории и внедрение её в практику научных и прикладных исследований, по нашему мнению будет иметь значение не только для общей теории информации, но и для тех предметных областей, где объекты познания представимы в виде дискретных систем, состоящих из конечного множества элементов. Не исключено, что одной из таких областей, в числе первых, может стать статистическая термодинамика, полемика вокруг непосредственной взаимосвязи которой, с вероятностной теорией информации Шеннона, идёт уже далеко не один десяток лет. Поэтому, одним из актуальных направлений дальнейших исследований, нам видится информационно-синергетический анализ термодинамических систем в процессе их перехода из структурно-упорядоченного состояния в состояние термодинамического равновесия.

Литература

1.      Вяткин В.Б. Синергетическая теория информации. Часть 1. Синергетический подход к определению количества информации // Научный журнал КубГАУ [Электронный ресурс]. – Краснодар: КубГАУ, 2008. – №44(10). Режим доступа: http://ej.kubagro.ru/2008/10/pdf/12.pdf

2.      Шеннон К. Работы по теории информации и кибернетике. – М.: Изд. иностр. лит., 1963. – 830с.

3.      Харкевич А.А. Очерки общей теории связи. – М.: Гостехиздат, 1955. – 268с.

4.      Новик И.Б. Негэнтропия и количество информации // Вопросы философии. – 1962, № 6. – С.118-128.

5.      Колмогоров А.Н. Теория информации и теория алгоритмов. – М.: Наука, 1987. – 304с.

6.      Хартли Р.В.Л. Передача информации. // Сб.: Теория информации и ее приложения. – М.: Физматгиз, 1959. – С. 5-35.

7.      Колмогоров А.Н. Три подхода к определению понятия «количество информации» // Проблемы передачи информации. – 1965, т.1, №1 – С. 3-11.